Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 43 trang 78 sách bài tập Toán 12 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải các bài tập Toán 12 có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 43 trang 78 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
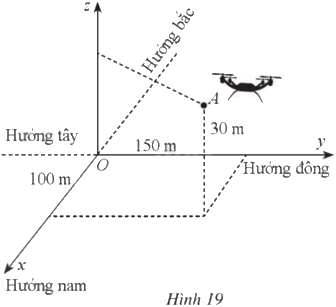
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí (A) cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m (Hình 19). Để thực hiện nhiệm vụ tiếp theo, người điều khiển flycam đến vị trí (B) cách vị trí điều khiển 80 m về phía bắc và 120 m về phía tây, đồng thời cách mặt đất 50 m. Chọn hệ trục toạ độ (Oxyz) với gốc (O) là vị trí người điều khiển, mặt phẳng (left( {Oxy} right)) trùng
Đề bài
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí \(A\) cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m (Hình 19). Để thực hiện nhiệm vụ tiếp theo, người điều khiển flycam đến vị trí \(B\) cách vị trí điều khiển 80 m về phía bắc và 120 m về phía tây, đồng thời cách mặt đất 50 m.
Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) là vị trí người điều khiển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) có hướng trùng với hướng nam, trục \(Oy\) có hướng trùng với hướng đông, trục \(Oz\) vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên các trục tương ứng với 1 m.
a) Xác định toạ độ của flycam tại mỗi vị trí \(A,B\) đối với hệ toạ độ đã chọn.
b) Tính quãng đường flycam bay từ vị trí \(A\) đến vị trí \(B\), biết flycam bay từ vị trí \(A\) đến vị trí \(B\) theo một đường thẳng (làm tròn kết quả đến hàng đơn vị của mét).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính độ dài đoạn thẳng \(AB\):
\(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Lời giải chi tiết
a) Toạ độ của flycam tại vị trí \(A\) là \(\left( {100;150;30} \right)\).
Toạ độ của flycam tại vị trí \(B\) là \(\left( { - 80; - 120;50} \right)\).
b) Quãng đường flycam bay từ vị trí \(A\) đến vị trí \(B\) bằng khoảng cách giữa hai điểm \(A\) và \(B\) bằng: \(AB = \sqrt {\left( { - 80 - 100} \right)2 + \left( { - 120 - 150} \right)2 + \left( {50 - 30} \right)} = \sqrt {105700} \approx 325\left( m \right)\).
Vậy quãng đường flycam bay từ vị trí \(A\) đến vị trí \(B\) bằng 325 m.
Bài 43 trang 78 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường tập trung vào việc vận dụng các quy tắc đạo hàm cơ bản để tính đạo hàm của các hàm số phức tạp hơn, bao gồm hàm hợp, hàm lượng giác, hàm mũ, hàm logarit. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, điểm uốn, và ứng dụng của đạo hàm trong các lĩnh vực khác.
Bài 43 thường bao gồm các dạng bài tập sau:
Ví dụ: Tính đạo hàm của hàm số y = sin2(2x + 1).
Lời giải:
Sử dụng quy tắc đạo hàm hàm hợp, ta có:
y' = 2sin(2x + 1) * cos(2x + 1) * 2 = 4sin(2x + 1)cos(2x + 1) = 2sin(4x + 2)
Để học tốt môn Toán 12 và giải các bài tập về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Hãy bắt đầu với các bài tập cơ bản và dần dần nâng cao độ khó. Đừng ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn.
Bài 43 trang 78 sách bài tập Toán 12 Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin hơn trong việc học Toán 12 và đạt kết quả tốt trong các kỳ thi.