Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 70 trang 35 Sách bài tập Toán 12 - Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 70 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Đồ thị hàm số \(y = \frac{{2{\rm{x}}}}{{x + 1}}\) là đường cong nào trong các đường cong sau?
Đề bài
Đồ thị hàm số \(y = \frac{{2{\rm{x}}}}{{x + 1}}\) là đường cong nào trong các đường cong sau?
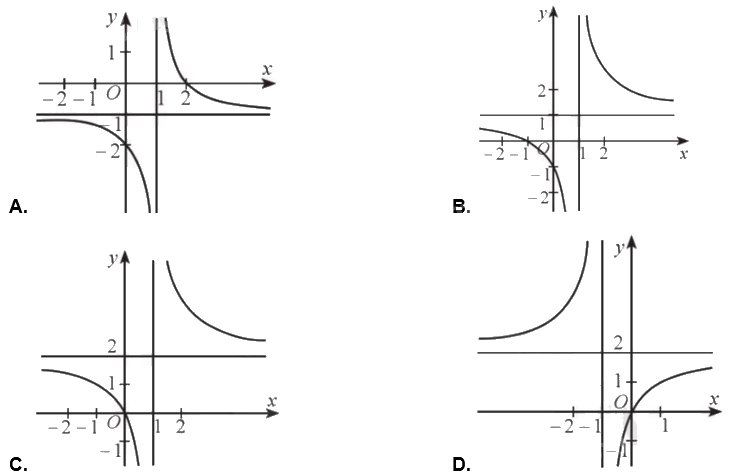
Phương pháp giải - Xem chi tiết
‒ Xét các đường tiệm cận của đồ thị hàm số.
Lời giải chi tiết
Đồ thị hàm số \(y = \frac{{2{\rm{x}}}}{{x + 1}}\) có tiệm cận đứng là đường thẳng \(x = - 1\) và tiệm cận ngang là đường thẳng \(y = 2\).
Chọn D.
Bài 70 trang 35 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các công thức và phương pháp giải toán đã được học.
Bài 70 thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 70 trang 35 Sách bài tập Toán 12 - Cánh Diều một cách hiệu quả, bạn cần:
Đề bài: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
Bước 1: Tính đạo hàm của hàm số:
y' = 3x2 - 6x
Bước 2: Tìm các điểm làm đạo hàm bằng 0:
3x2 - 6x = 0
=> 3x(x - 2) = 0
=> x = 0 hoặc x = 2
Bước 3: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Bước 4: Kết luận:
Hàm số đạt cực đại tại x = 0, ycđ = 2.
Hàm số đạt cực tiểu tại x = 2, yct = -2.
Vậy, các điểm cực trị của hàm số là (0; 2) và (2; -2).
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm các bài tập tương tự trong Sách bài tập Toán 12 - Cánh Diều và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các khóa học Toán 12 online tại giaitoan.edu.vn để được hướng dẫn và giải đáp thắc mắc bởi các giáo viên giàu kinh nghiệm.
Việc giải bài tập Toán 12 đóng vai trò quan trọng trong việc chuẩn bị cho kỳ thi THPT Quốc gia. Thông qua việc giải bài tập, bạn có thể:
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải bài 70 trang 35 Sách bài tập Toán 12 - Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt!