Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 1 trang 111, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn chinh phục môn Toán một cách hiệu quả.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao? b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Đề bài
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất của ba đường phân giác trong tam giác: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.
b) Dựa vào chứng minh các cặp tam giác bằng nhau.
Lời giải chi tiết
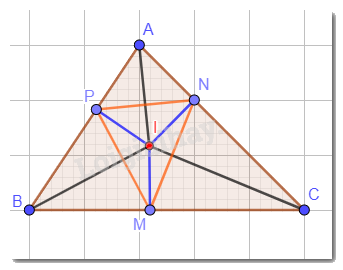
a) Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Vậy các tam giác IMN, INP, IPM có là tam giác cân tại I.
b)
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông). Suy ra: CN = CM ( 2 cạnh tương ứng).
Vậy tam giác CMN có là tam giác cân.
Tương tự, ta có: AP = AN; BP = BM.
Vậy các tam giác ANP, BPM, CMN có là tam giác cân.
Bài 1 trang 111 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về tam giác cân, tính chất đường trung tuyến trong tam giác, và các định lý liên quan đến góc trong tam giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết vấn đề.
Bài 1 yêu cầu học sinh chứng minh một số tính chất liên quan đến tam giác cân và đường trung tuyến. Cụ thể, bài tập thường xoay quanh việc chứng minh hai tam giác bằng nhau, từ đó suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau. Việc hiểu rõ các tiêu chí xét tam giác bằng nhau (cạnh - cạnh - cạnh, góc - cạnh - góc, góc - góc - cạnh) là vô cùng quan trọng.
Để giải bài 1 trang 111 SGK Toán 7 tập 2 - Cánh diều, bạn có thể áp dụng các phương pháp sau:
(a) Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD là đường phân giác của góc BAC.
Chứng minh:
(b) Cho tam giác ABC cân tại B. Gọi M là trung điểm của AC. Chứng minh BM là đường cao của tam giác ABC.
Chứng minh:
Để củng cố kiến thức về tam giác cân và đường trung tuyến, bạn có thể giải thêm các bài tập tương tự trong SGK và sách bài tập Toán 7 tập 2 - Cánh diều. Ngoài ra, bạn có thể tìm hiểu thêm về các loại đường trung tuyến khác trong tam giác (đường trung tuyến đi qua đỉnh, đường trung tuyến đi qua trung điểm cạnh) và các tính chất liên quan.
Bài 1 trang 111 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tam giác cân và đường trung tuyến. Bằng cách nắm vững các kiến thức cơ bản và phương pháp giải quyết vấn đề, bạn có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.