Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 96 SGK Toán 7 tập 2 - Cánh diều. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:
Đề bài
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:
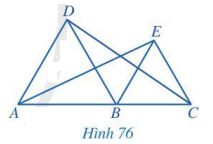
a) AD // BE và BD // CE;
b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
c) AE = CD.
Phương pháp giải - Xem chi tiết
a) Ta chứng minh AD // BE và BD // CE dựa vào các cặp góc bằng nhau ở vị trí đồng vị.
b) Chứng minh \(\widehat {ABE} = \widehat {DBC} = 120^\circ \) dựa vào số đo góc của ba điểm thẳng hàng là 180°.
c) Chứng minh AE = CD bằng cách chứng minh tam giác ABE bằng tam giác DBC
Lời giải chi tiết
a)
Tam giác ABD và BCE là tam giác đều nên \(\widehat {EBC} = \widehat {DAB} = 60^\circ \)
Vì A, B, C thẳng hàng nên \(\widehat {DAB}= \widehat {DAC}\) suy ra \(\widehat {EBC} = \widehat {DAB}\).
Mà góc EBC và góc DAC ở vị trí đồng vị nên AD // BE.
Tam giác ABD và BCE là tam giác đều nên \(\widehat {DBA} = \widehat {ECB} = 60^\circ \)
Vì A, B, C thẳng hàng nên \(\widehat {ECB}= \widehat {ECA}\) suy ra \(\widehat {DBA} = \widehat {ECB}\).
Mà góc DBA và góc ECA ở vị trí đồng vị nên BD // CE.
b) Ta có A, B, C thẳng hàng nên góc ABC bằng 180°. Mà \(\widehat {DBA} = \widehat {EBC} = 60^\circ \Rightarrow \widehat {DBE} = 60^\circ \).
Vậy \(\widehat {ABE} = \widehat {DBC} = 120^\circ \) (\(\widehat {ABE} = \widehat {DBA} + \widehat {DBE};\widehat {DBC} = \widehat {DBE} + \widehat {EBC}\)).
c) Tam giác ABD và BCE là tam giác đều
\(\Rightarrow AB=AD, BE=BC\)
Xét hai tam giác ABE và DBC có:
AB = DB;
\(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
BE = BC.
\(\Rightarrow \Delta ABE = \Delta DBC\) (c.g.c)
Do đó, AE = DC ( 2 cạnh tương ứng).
\(\widehat {ABE} = \widehat {DBC} = 120^\circ \)
Bài 4 trang 96 SGK Toán 7 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán liên quan đến tính chất của góc.
Để giải bài 4 trang 96 SGK Toán 7 tập 2 - Cánh diều, các em cần:
Bài 4: Cho hình vẽ sau (hình vẽ minh họa với hai đường thẳng song song a và b bị cắt bởi đường thẳng c). Biết góc A1 = 60o. Tính các góc còn lại.
Lời giải:
Để củng cố kiến thức về bài 4 trang 96 SGK Toán 7 tập 2 - Cánh diều, các em có thể tự giải các bài tập sau:
Bài 4 trang 96 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng giúp các em hiểu rõ hơn về các tính chất của góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Việc nắm vững lý thuyết và phương pháp giải bài tập sẽ giúp các em tự tin hơn trong quá trình học tập môn Toán.