Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục II trang 53 và 54 sách giáo khoa Toán 7 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài học, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
a) Cho tỉ lệ thức 6/10=-9/-15. So sánh tích hai số hạng 6 và -15 với tích hai số hạng 10 và -9 Tìm số x trong tỉ lệ thức sau: (-0,4) : x = 1,2 : 0,3
a) Cho tỉ lệ thức \(\frac{6}{{10}} = \frac{{ - 9}}{{ - 15}}\). So sánh tích hai số hạng 6 và -15 với tích hai số hạng 10 và -9
b) Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Nhân hai vế của tỉ lệ thức với tích bd, ta được đẳng thức nào?
Phương pháp giải:
a) Tính các tích rồi so sánh
b) Nhân hai vế của tỉ lệ thức với tích bd, ta được đẳng thức mới
Lời giải chi tiết:
a) Ta có: 6. (-15) = -90;
10.(-9) = = - 90
Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9
b) Nhân hai vế của tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với tích bd, ta được: \(\frac{{a.b.d}}{b} = \frac{{c.b.d}}{d} \Rightarrow ad = bc\)
Vậy ta được đẳng thức ad = bc
Tìm số x trong tỉ lệ thức sau:
(-0,4) : x = 1,2 : 0,3
Phương pháp giải:
Sử dụng tính chất của tỉ lệ thức:
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì ad = bc
Lời giải chi tiết:
Vì (-0,4) : x = 1,2 : 0,3 nên \(\frac{{ - 0,4}}{x} = \frac{{1,2}}{{0,3}} \Rightarrow ( - 0,4).0,3 = 1,2.x \Rightarrow x = \frac{{( - 0,4).0,3}}{{1,2}} = - 0,1\)
Vậy x = - 0,1
a) Đưa hai số 21 và 27 vào  cho thích hợp:
cho thích hợp:
18 .  =
=  . 14
. 14
b) Lập tất cả các tỉ lệ thức có thể được từ bốn số sau:
14; 18; 21; 27.
Phương pháp giải:
+ Tìm đẳng thức a.d = b.c có được từ 4 số a,b,c,d khác 0
+ Nếu ad = bc thì ta có 4 tỉ lệ thức: \(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\)
Lời giải chi tiết:
a) Ta được: 18 . 21 = 27 . 14
b) Từ 4 số: 14; 18; 21; 27, ta có đẳng thức sau: 18 . 27 = 21 . 14, ta lập được các tỉ lệ thức:
\(\frac{{18}}{{27}} = \frac{{14}}{{21}};\frac{{18}}{{14}} = \frac{{27}}{{21}};\frac{{14}}{{18}} = \frac{{21}}{{27}};\frac{{21}}{{14}} = \frac{{27}}{{18}}\)
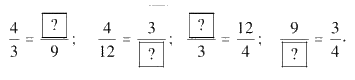
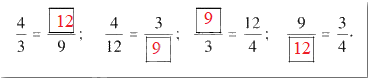
Ta có đẳng thức 4 : 9 = 3 . 12
a) Viết kết quả dưới dạng tỉ lệ thức khi chia hai vế của đẳng thức trên cho 9.3.
b) Tìm số thích hợp cho 
Phương pháp giải:
Sử dụng tính chất của tỉ lệ thức:
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì ad = bc
Lời giải chi tiết:
a) Cho tỉ lệ thức \(\frac{6}{{10}} = \frac{{ - 9}}{{ - 15}}\). So sánh tích hai số hạng 6 và -15 với tích hai số hạng 10 và -9
b) Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Nhân hai vế của tỉ lệ thức với tích bd, ta được đẳng thức nào?
Phương pháp giải:
a) Tính các tích rồi so sánh
b) Nhân hai vế của tỉ lệ thức với tích bd, ta được đẳng thức mới
Lời giải chi tiết:
a) Ta có: 6. (-15) = -90;
10.(-9) = = - 90
Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9
b) Nhân hai vế của tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với tích bd, ta được: \(\frac{{a.b.d}}{b} = \frac{{c.b.d}}{d} \Rightarrow ad = bc\)
Vậy ta được đẳng thức ad = bc
Tìm số x trong tỉ lệ thức sau:
(-0,4) : x = 1,2 : 0,3
Phương pháp giải:
Sử dụng tính chất của tỉ lệ thức:
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì ad = bc
Lời giải chi tiết:
Vì (-0,4) : x = 1,2 : 0,3 nên \(\frac{{ - 0,4}}{x} = \frac{{1,2}}{{0,3}} \Rightarrow ( - 0,4).0,3 = 1,2.x \Rightarrow x = \frac{{( - 0,4).0,3}}{{1,2}} = - 0,1\)
Vậy x = - 0,1
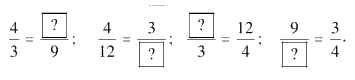
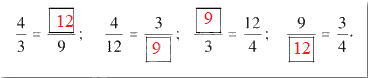
Ta có đẳng thức 4 : 9 = 3 . 12
a) Viết kết quả dưới dạng tỉ lệ thức khi chia hai vế của đẳng thức trên cho 9.3.
b) Tìm số thích hợp cho 
Phương pháp giải:
Sử dụng tính chất của tỉ lệ thức:
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì ad = bc
Lời giải chi tiết:
a) Đưa hai số 21 và 27 vào  cho thích hợp:
cho thích hợp:
18 .  =
=  . 14
. 14
b) Lập tất cả các tỉ lệ thức có thể được từ bốn số sau:
14; 18; 21; 27.
Phương pháp giải:
+ Tìm đẳng thức a.d = b.c có được từ 4 số a,b,c,d khác 0
+ Nếu ad = bc thì ta có 4 tỉ lệ thức: \(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\)
Lời giải chi tiết:
a) Ta được: 18 . 21 = 27 . 14
b) Từ 4 số: 14; 18; 21; 27, ta có đẳng thức sau: 18 . 27 = 21 . 14, ta lập được các tỉ lệ thức:
\(\frac{{18}}{{27}} = \frac{{14}}{{21}};\frac{{18}}{{14}} = \frac{{27}}{{21}};\frac{{14}}{{18}} = \frac{{21}}{{27}};\frac{{21}}{{14}} = \frac{{27}}{{18}}\)
Mục II trong SGK Toán 7 tập 1 - Cánh diều tập trung vào các kiến thức về số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố và ứng dụng của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học tiếp theo trong chương trình Toán 7.
Bài 1 yêu cầu học sinh xác định các số nguyên tố, hợp số trong một dãy số cho trước. Để làm được bài này, học sinh cần nắm vững định nghĩa về số nguyên tố (chỉ chia hết cho 1 và chính nó) và hợp số (chia hết cho ít nhất ba số tự nhiên khác nhau).
Ví dụ:
Bài 2 hướng dẫn học sinh phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố. Đây là một kỹ năng quan trọng trong việc đơn giản hóa biểu thức và giải quyết các bài toán liên quan đến số học.
Ví dụ: Phân tích số 36 ra thừa số nguyên tố:
Bài 3 yêu cầu học sinh sử dụng kiến thức về phân tích ra thừa số nguyên tố để giải quyết các bài toán thực tế, chẳng hạn như tìm ước chung lớn nhất (ƯCLN) và bội chung nhỏ nhất (BCNN) của hai hoặc nhiều số.
Ví dụ: Tìm ƯCLN của 24 và 36:
Để giải bài tập trong mục II trang 53, 54 SGK Toán 7 tập 1 - Cánh diều một cách hiệu quả, học sinh cần:
Để củng cố kiến thức và nâng cao kỹ năng giải toán, học sinh có thể tự giải các bài tập sau:
Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, các em học sinh đã có thể tự tin giải các bài tập trong mục II trang 53, 54 SGK Toán 7 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!