Chào mừng bạn đến với bài học về Lý thuyết Đại lượng tỉ lệ nghịch trong chương trình Toán 7 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về mối quan hệ tỉ lệ nghịch giữa hai đại lượng.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, và cách áp dụng lý thuyết này vào giải các bài toán thực tế. Hãy chuẩn bị sẵn sàng để khám phá thế giới toán học thú vị này!
I. Khái niệm
I. Khái niệm
Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay x.y = a (a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a
Chú ý: Nếu đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a thì đại lượng x cũng tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ a. Ta nói x và y là hai đại lượng tỉ lệ nghịch với nhau.
II. Tính chất
Nếu 2 đại lượng tỉ lệ nghịch với nhau thì:
+ Tích hai đại lượng tương ứng của chúng luôn không đổi ( bằng hệ số tỉ lệ).
+ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo tỉ số hai giá trị tương ứng của đại lượng kia.
Cụ thể: Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a. Với mỗi giá trị x1 , x2 , x3 ,… khác 0 của x, lần lượt tương ứng với giá trị y1 , y2 , y3 ,… của y thì:
Ví dụ:
Vì v. t = s không đổi nên vận tốc và thời gian ô tô đi là 2 đại lượng tỉ lệ nghịch
Theo tính chất 2 đại lượng tỉ lệ nghịch, ta có:
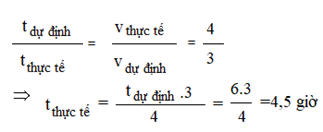
Trong chương trình Toán 7, phần Đại lượng tỉ lệ nghịch là một kiến thức nền tảng quan trọng. Hiểu rõ lý thuyết này sẽ giúp học sinh giải quyết nhiều bài toán thực tế và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Hai đại lượng x và y được gọi là tỉ lệ nghịch với nhau nếu tích xy = a (a là một hằng số khác 0). Hằng số a được gọi là hệ số tỉ lệ. Khi đó, ta có công thức: y = a/x.
Để nhận biết hai đại lượng x và y tỉ lệ nghịch, ta cần kiểm tra xem tích xy có là một hằng số khác 0 hay không. Nếu xy = a (a ≠ 0) thì x và y tỉ lệ nghịch.
Ví dụ 1: Quãng đường đi được của một ô tô tỉ lệ nghịch với thời gian đi. Nếu ô tô đi được 120km trong 2 giờ, thì vận tốc của ô tô là bao nhiêu? Thời gian ô tô đi hết quãng đường 180km là bao lâu?
Giải:
Gọi quãng đường là s (km) và thời gian là t (giờ). Ta có s = vt (v là vận tốc). Vì vận tốc v không đổi, nên s và t tỉ lệ thuận với nhau. Tuy nhiên, nếu bài toán yêu cầu thời gian đi tỉ lệ nghịch với vận tốc, thì ta có s = vt, và t = s/v. Nếu s không đổi, thì t và v tỉ lệ nghịch.
Ví dụ 2: Số công nhân làm một công việc tỉ lệ nghịch với thời gian hoàn thành công việc. Nếu 5 công nhân làm xong công việc trong 10 ngày, thì 10 công nhân làm xong công việc trong bao lâu?
Giải:
Gọi số công nhân là n và thời gian hoàn thành công việc là t. Ta có n * t = a (a là tổng số công việc). Trong trường hợp này, a là một hằng số. Vậy n và t tỉ lệ nghịch.
Ta có: 5 * 10 = 50. Vậy 10 * t = 50, suy ra t = 5 ngày.
Bài 1: Hai đại lượng x và y tỉ lệ nghịch với nhau. Khi x = 2 thì y = 6. Hãy tìm y khi x = 3.
Bài 2: Một đội công nhân có 15 người sửa một đoạn đường trong 6 ngày. Hỏi nếu đội công nhân đó có 10 người thì sửa đoạn đường đó trong bao lâu?
Lý thuyết Đại lượng tỉ lệ nghịch có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như vật lý, hóa học, kinh tế,... Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Đại lượng tỉ lệ nghịch Toán 7 Cánh diều. Chúc bạn học tập tốt!