Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục II trang 109 và 110 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
II. Tính chất ba đường phân giác của tam giác
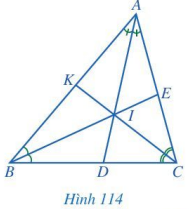
Quan sát các đường phân giác AD, BE, CK của tam giác ABC(Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 114 để xem các đường phân giác AD, BE, CK có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Các đường phân giác AD, BE, CK có cùng đi qua một điểm là điểm I.
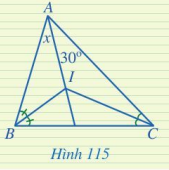
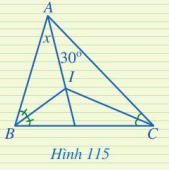
Tìm số đo x trong Hình 115.
Phương pháp giải:
Dựa vào tính chất của ba đường phân giác trong tam giác.
Lời giải chi tiết:
I là giao điểm của hai đường phân giác góc B và góc C.
Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C.
Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \).
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Phương pháp giải:
Dựa vào tính chất của ba đường phân giác trong tam giác và tính chất của đường trung tuyến (đi qua trung điểm và vuông góc tại trung điểm).
Lời giải chi tiết:
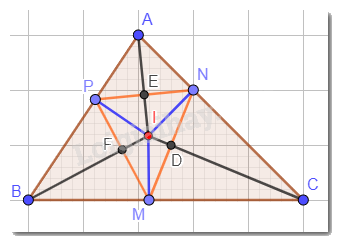
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
II. Tính chất ba đường phân giác của tam giác
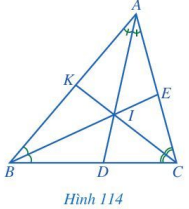
Quan sát các đường phân giác AD, BE, CK của tam giác ABC(Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 114 để xem các đường phân giác AD, BE, CK có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Các đường phân giác AD, BE, CK có cùng đi qua một điểm là điểm I.
Tìm số đo x trong Hình 115.
Phương pháp giải:
Dựa vào tính chất của ba đường phân giác trong tam giác.
Lời giải chi tiết:
I là giao điểm của hai đường phân giác góc B và góc C.
Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C.
Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \).
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Phương pháp giải:
Dựa vào tính chất của ba đường phân giác trong tam giác và tính chất của đường trung tuyến (đi qua trung điểm và vuông góc tại trung điểm).
Lời giải chi tiết:
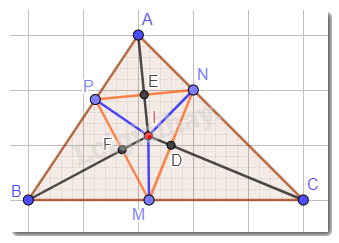
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
Mục II trong SGK Toán 7 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như các định lý liên quan đến tam giác, các trường hợp đồng dạng của tam giác, hoặc các ứng dụng của tam giác đồng dạng. Việc nắm vững kiến thức lý thuyết và kỹ năng vận dụng là vô cùng quan trọng để giải quyết các bài tập trong mục này.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về một định lý hoặc tính chất đã học để chứng minh một đẳng thức hoặc một mối quan hệ hình học. Để giải bài tập này, các em cần:
Bài tập này có thể yêu cầu học sinh tính toán một giá trị cụ thể, ví dụ như độ dài một đoạn thẳng, số đo một góc, hoặc diện tích một hình. Để giải bài tập này, các em cần:
Bài tập này thường là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một vấn đề trong cuộc sống. Để giải bài tập này, các em cần:
Để giải bài tập Toán 7 tập 2 - Cánh diều một cách hiệu quả, các em nên:
Giả sử bài tập yêu cầu chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh (c-g-c). Các em cần:
Xét hai tam giác ABC và DEF, ta có:
Vậy, ΔABC = ΔDEF (c-g-c)
Việc giải bài tập mục II trang 109, 110 SGK Toán 7 tập 2 - Cánh diều đòi hỏi sự hiểu biết vững chắc về kiến thức lý thuyết và kỹ năng vận dụng linh hoạt. Hy vọng rằng với những hướng dẫn chi tiết và lời khuyên hữu ích trên đây, các em sẽ tự tin chinh phục các bài tập Toán 7 và đạt kết quả tốt nhất.
| Bài tập | Mức độ khó | Gợi ý giải |
|---|---|---|
| Bài 1 | Trung bình | Vận dụng định lý... |
| Bài 2 | Khó | Sử dụng công thức... |
| Bài 3 | Trung bình | Xây dựng mô hình... |