Chào mừng bạn đến với bài học về Lý thuyết Hai tam giác bằng nhau trong chương trình Toán 7 - Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai tam giác bằng nhau, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu các trường hợp bằng nhau của hai tam giác, các yếu tố cần thiết để chứng minh hai tam giác bằng nhau, và ứng dụng của lý thuyết này trong việc giải toán.
Hai tam giác bằng nhau
Hai tam giác bằng nhau
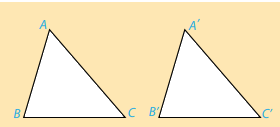
Hai tam giác ABC và A’B’C’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, tức là:
AB = A’B’ ; AC = A’C’ ; BC = B’C’ và \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
Ta viết: \(\Delta ABC = \Delta A'B'C'\)
Nếu 2 tam giác bằng nhau, ta suy ra tất cả các cạnh, các góc tương ứng bằng nhau.
Trong chương trình Toán 7, kiến thức về hai tam giác bằng nhau là nền tảng quan trọng để học tập các kiến thức hình học tiếp theo. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và bài tập vận dụng để giúp học sinh nắm vững kiến thức này.
Hai tam giác được gọi là bằng nhau nếu chúng có tất cả các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau. Điều này có nghĩa là nếu bạn có thể “ghép” hai tam giác lên nhau sao cho chúng hoàn toàn trùng khớp, thì chúng bằng nhau.
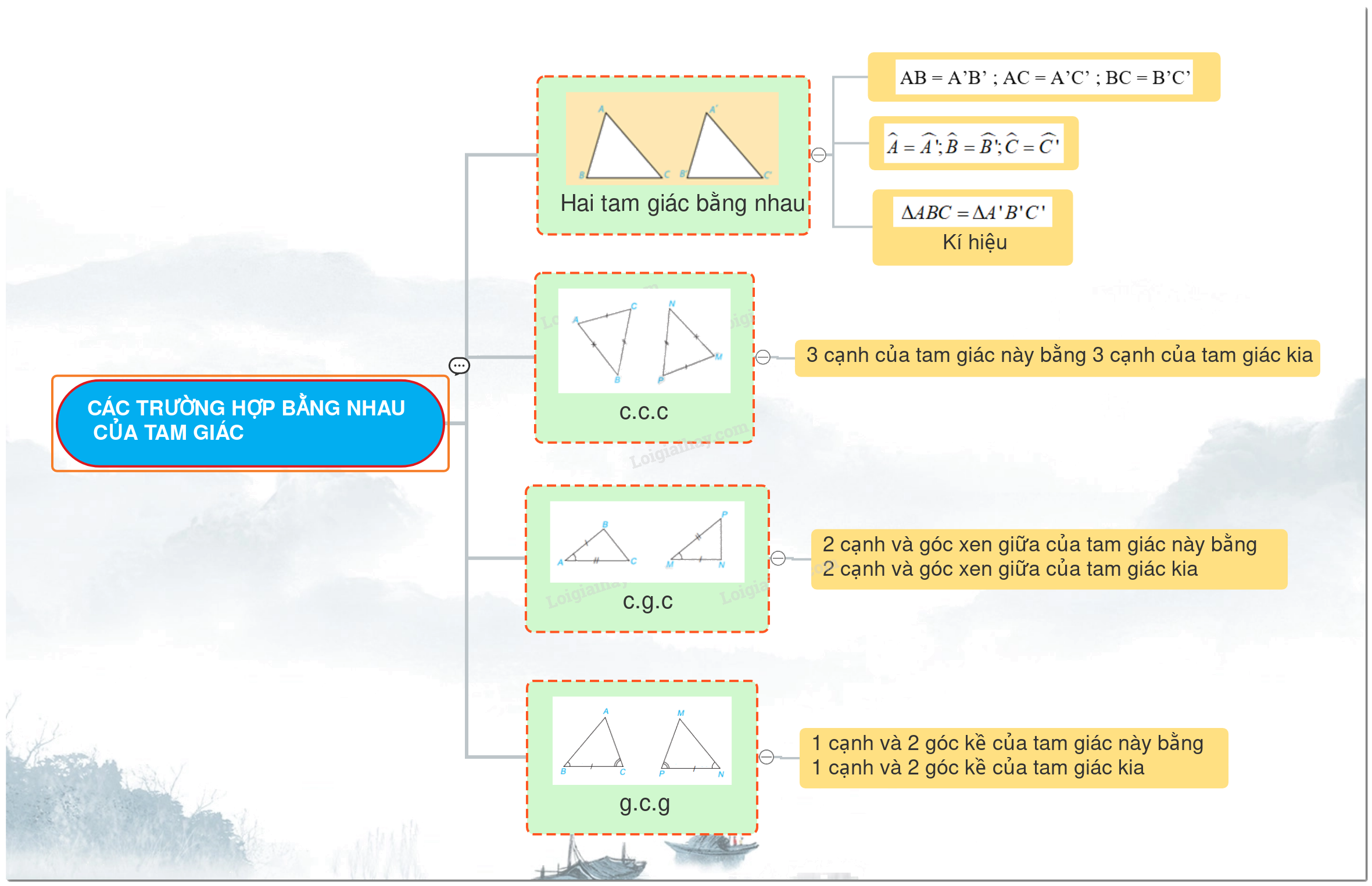
Có ba trường hợp bằng nhau của hai tam giác thường được sử dụng:
Lý thuyết hai tam giác bằng nhau được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau, hoặc chứng minh một điểm nằm trên một đường thẳng.
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE, BC = EF, CA = FD. Chứng minh rằng tam giác ABC bằng tam giác DEF.
Giải:
Vì AB = DE, BC = EF, CA = FD (giả thiết) nên theo trường hợp bằng nhau cạnh - cạnh - cạnh (c-c-c), ta có tam giác ABC bằng tam giác DEF.
Ví dụ 2: Cho tam giác MNP và tam giác RST có MN = RS, góc N = góc S, NP = ST. Chứng minh rằng tam giác MNP bằng tam giác RST.
Giải:
Vì MN = RS, góc N = góc S, NP = ST (giả thiết) nên theo trường hợp bằng nhau cạnh - góc - cạnh (c-g-c), ta có tam giác MNP bằng tam giác RST.
Bài 1: Cho tam giác PQR và tam giác UVW có PQ = UV, QR = VW, RP = WU. Chứng minh rằng tam giác PQR bằng tam giác UVW.
Bài 2: Cho tam giác XYZ và tam giác ABC có XY = AB, góc X = góc A, YZ = BC. Chứng minh rằng tam giác XYZ bằng tam giác ABC.
Bài 3: Cho tam giác DEF và tam giác MNP có góc D = góc M, DE = MP, góc E = góc N. Chứng minh rằng tam giác DEF bằng tam giác MNP.
Lý thuyết hai tam giác bằng nhau là một phần quan trọng của chương trình Toán 7. Việc nắm vững lý thuyết và các trường hợp bằng nhau của hai tam giác sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.