Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 105 và 106 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
II. Tính chất ba đường trung tuyến của tam giác
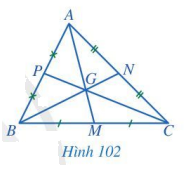
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 102 để xem ba đường trung tuyến có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.
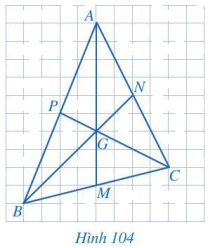
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
Phương pháp giải:
Quan sát Hình 104 rồi đếm số ô vuông của mỗi cạnh tương ứng để đưa ra các tỉ số.
Lời giải chi tiết:
Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
Phương pháp giải:
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
Lời giải chi tiết:
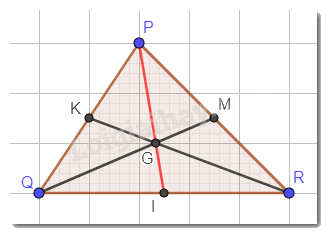
Ta có G là giao điểm của hai đường trung tuyến QM và RK.
Mà I là trung điểm của QR nên PI cũng là đường trung tuyến trong tam giác PQR.
Vậy PI giao với QM và RK tại G
Do đó, G thuộc PI hay ba điểm P,G, I thẳng hàng.
II. Tính chất ba đường trung tuyến của tam giác
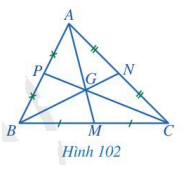
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 102 để xem ba đường trung tuyến có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
Phương pháp giải:
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
Lời giải chi tiết:
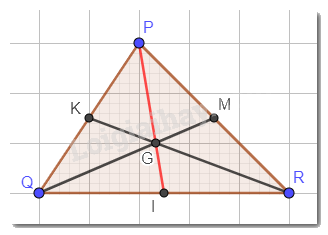
Ta có G là giao điểm của hai đường trung tuyến QM và RK.
Mà I là trung điểm của QR nên PI cũng là đường trung tuyến trong tam giác PQR.
Vậy PI giao với QM và RK tại G
Do đó, G thuộc PI hay ba điểm P,G, I thẳng hàng.
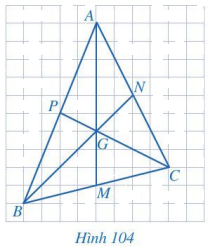
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
Phương pháp giải:
Quan sát Hình 104 rồi đếm số ô vuông của mỗi cạnh tương ứng để đưa ra các tỉ số.
Lời giải chi tiết:
Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).
Mục II trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức đã học về tam giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tam giác, đặc biệt là các bài toán về tổng ba góc trong một tam giác, quan hệ giữa góc và cạnh đối diện trong tam giác.
Bài 1 thường là các bài tập trắc nghiệm hoặc điền vào chỗ trống để kiểm tra kiến thức cơ bản về tam giác. Các em cần nắm vững các khái niệm như tam giác là gì, các loại tam giác (tam giác đều, tam giác cân, tam giác vuông), các yếu tố của tam giác (góc, cạnh).
Bài 2 yêu cầu học sinh tính góc còn lại của một tam giác khi biết hai góc. Để giải bài này, các em cần nhớ định lý về tổng ba góc trong một tam giác: tổng ba góc trong một tam giác bằng 180 độ.
Ví dụ:
Bài 3 thường yêu cầu học sinh so sánh độ dài các cạnh của một tam giác dựa vào số đo các góc đối diện. Các em cần nhớ quy tắc:
Ví dụ:
Để giải các bài tập trong mục II trang 105, 106 SGK Toán 7 tập 2 - Cánh diều một cách hiệu quả, các em cần:
Khi giải các bài tập về tam giác, các em cần chú ý đến đơn vị đo góc (độ) và đơn vị đo độ dài (cm, m, km...). Ngoài ra, các em cũng cần chú ý đến việc sử dụng đúng các ký hiệu toán học để tránh gây nhầm lẫn.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tự tìm thêm các bài tập tương tự trong các sách bài tập hoặc trên internet. Ngoài ra, các em cũng có thể tham khảo các bài giảng online hoặc tìm kiếm sự giúp đỡ của giáo viên, bạn bè.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập trong mục II trang 105, 106 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt!