Chào mừng các em học sinh đến với bài học về Lý thuyết Số vô tỉ và Căn bậc hai số học trong chương trình Toán 7 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng về các khái niệm này, giúp các em hiểu rõ hơn về thế giới số học.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho các em những bài giảng chất lượng, dễ hiểu và nhiều bài tập thực hành để các em có thể tự tin làm chủ môn Toán.
I. Số vô tỉ
I. Số vô tỉ
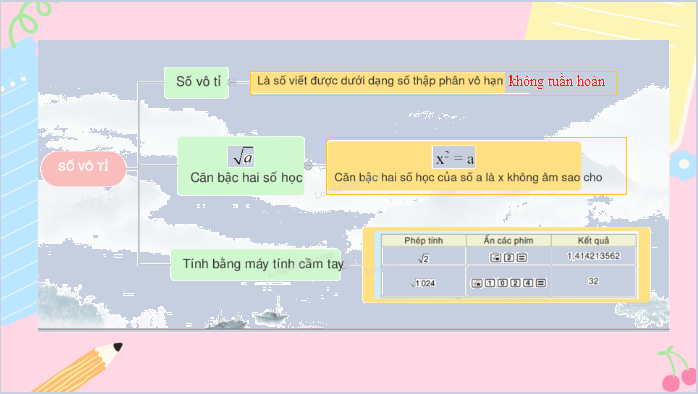
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Ví dụ: \(\pi = 3,1415926.....;e = 2,71828.....;....\) là những số vô tỉ
II. Căn bậc hai số học
Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho x2 = a.
Ví dụ: \(\sqrt {121} = 11\) vì 11 > 0 và 112 = 121
Chú ý: Cho \(a \ge 0\). Khi đó:
+ Đẳng thức \(\sqrt a = b\) đúng nếu \(b \ge 0;{b^2} = a\)
+ \({\left( {\sqrt a } \right)^2} = a\)
Trong chương trình Toán 7, việc làm quen với khái niệm số vô tỉ và căn bậc hai số học là một bước tiến quan trọng trong việc xây dựng nền tảng toán học vững chắc. Bài viết này sẽ trình bày chi tiết về lý thuyết, ví dụ minh họa và các bài tập ứng dụng để giúp các em học sinh hiểu rõ hơn về chủ đề này.
Số vô tỉ là những số không thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b khác 0. Nói cách khác, số vô tỉ là những số thập phân vô hạn không tuần hoàn. Ví dụ:
Các số vô tỉ xuất hiện trong nhiều lĩnh vực của toán học và khoa học, và việc hiểu rõ về chúng là rất quan trọng.
Căn bậc hai số học của một số a (không âm) là một số x sao cho x2 = a. Ký hiệu: √a. Ví dụ:
Lưu ý rằng căn bậc hai số học chỉ được định nghĩa cho các số không âm.
Nhiều số vô tỉ có thể được biểu diễn dưới dạng căn bậc hai. Ví dụ, √2 là một số vô tỉ. Tuy nhiên, không phải căn bậc hai nào cũng là số vô tỉ. Ví dụ, √9 = 3 là một số hữu tỉ.
Dưới đây là một số bài tập để các em luyện tập:
Số vô tỉ và căn bậc hai số học có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài học về Lý thuyết Số vô tỉ và Căn bậc hai số học Toán 7 Cánh diều đã cung cấp cho các em những kiến thức cơ bản và quan trọng về chủ đề này. Hy vọng rằng, thông qua bài viết này, các em sẽ hiểu rõ hơn về số vô tỉ, căn bậc hai số học và các ứng dụng của chúng. Chúc các em học tập tốt!
| Số | Căn bậc hai |
|---|---|
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| Bảng ví dụ về căn bậc hai của một số số nguyên. | |