Chào mừng các em học sinh đến với bài giải chi tiết mục I trang 108, 109 SGK Toán 7 tập 2 - Cánh diều. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em học sinh ôn tập và nắm vững kiến thức Toán học.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
I. Đường phân giác của tam giác
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.
Phương pháp giải:
Chứng minh dựa vào việc chứng minh hai tam giác bằng nhau.
Lời giải chi tiết:
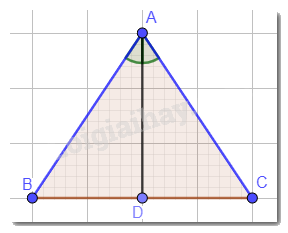
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?
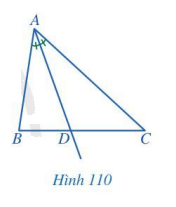
Phương pháp giải:
Quan sát Hình 110 để đưa ra đặc điểm của hai đầu mút đoạn thẳng AD.
Lời giải chi tiết:
Các đầu mút của đoạn thẳng AD có đặc điểm: đầu mút A là đỉnh của tam giác, đầu mút D thuộc cạnh BC.
I. Đường phân giác của tam giác
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?
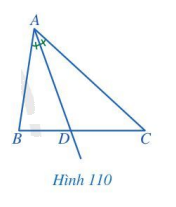
Phương pháp giải:
Quan sát Hình 110 để đưa ra đặc điểm của hai đầu mút đoạn thẳng AD.
Lời giải chi tiết:
Các đầu mút của đoạn thẳng AD có đặc điểm: đầu mút A là đỉnh của tam giác, đầu mút D thuộc cạnh BC.
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.
Phương pháp giải:
Chứng minh dựa vào việc chứng minh hai tam giác bằng nhau.
Lời giải chi tiết:
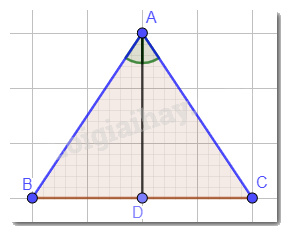
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
Mục I trang 108, 109 SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập chương I: Các số hữu tỉ. Đây là một phần quan trọng trong chương trình Toán 7, giúp học sinh củng cố kiến thức về các khái niệm cơ bản như số hữu tỉ, số nguyên, số thập phân, phân số, và các phép toán trên chúng.
Mục I bao gồm các bài tập rèn luyện kỹ năng:
Bài tập 1 yêu cầu học sinh điền vào chỗ trống để hoàn thiện các câu sau:
Lời giải:
Bài tập 2 yêu cầu học sinh xác định các số hữu tỉ trong tập hợp sau: {..., -3; -1,5; 0; 1,2; 3; ...}
Lời giải:
Các số hữu tỉ trong tập hợp trên là: -3; -1,5; 0; 1,2; 3.
Bài tập 3 yêu cầu học sinh biểu diễn các số hữu tỉ sau trên trục số: \frac{1}{2}; \frac{-1}{3}; 0; 1.
Lời giải:
(Hướng dẫn học sinh cách chia trục số thành các khoảng bằng nhau và xác định vị trí của các số hữu tỉ trên trục số)
Chương I: Các số hữu tỉ là nền tảng cho các chương học tiếp theo trong chương trình Toán 7. Việc nắm vững kiến thức về số hữu tỉ sẽ giúp học sinh dễ dàng tiếp thu các khái niệm và kỹ năng mới, đồng thời giải quyết các bài toán phức tạp hơn.
Hy vọng bài giải chi tiết mục I trang 108, 109 SGK Toán 7 tập 2 - Cánh diều này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!