Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục II trang 75 và 76 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững kiến thức và kỹ năng giải toán, từ đó đạt kết quả tốt nhất trong học tập.
II. Bất đẳng thức tam giác
Cho tam giác ABC có \(AB = 2\)cm, \(BC = 4\)cm. So sánh hai cạnh AC và AB.
Phương pháp giải:
Trong một tam giác, hiệu độ dài hai cạnh bất kì luôn nhỏ hơn độ dài cạnh còn lại.
Lời giải chi tiết:
Ta có: \(BC - AB = 4 - 2 = 2\).
Mà AC > BC - AB nên độ dài cạnh AC lớn hơn 2 hay AC > AB (vì \(AB = 2\)cm).
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có \(AB = 3\)cm, \(BC = 2\)cm, \(AC = 4\)cm.
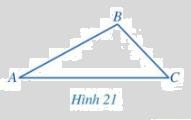
a) Hãy sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC mà bạn Thảo đã nói.
b) So sánh \(AB + BC\)và AC.
Phương pháp giải:
a) Học sinh sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC.
b) Dựa vào độ dài của các cạnh để so sánh \(AB + BC\) và AC.
Lời giải chi tiết:
a) Bạn Thảo nói đúng.
b) \(AB + BC = 3 + 2 = 5 > AC = 4\).
Vậy \(AB + BC\) > AC.
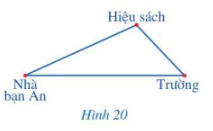
Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?
Phương pháp giải:
Học sinh có thể lấy thước đo (có chia kẻ vạch) để đo hai quãng đường rồi so sánh.
Lời giải chi tiết:
Bạn An đi đường đi thứ nhất là đường đi thẳng từ nhà đến trường sẽ gần hơn đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường.
II. Bất đẳng thức tam giác
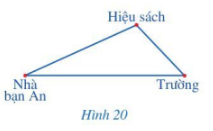
Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?
Phương pháp giải:
Học sinh có thể lấy thước đo (có chia kẻ vạch) để đo hai quãng đường rồi so sánh.
Lời giải chi tiết:
Bạn An đi đường đi thứ nhất là đường đi thẳng từ nhà đến trường sẽ gần hơn đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường.
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có \(AB = 3\)cm, \(BC = 2\)cm, \(AC = 4\)cm.
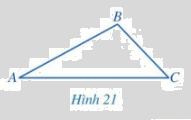
a) Hãy sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC mà bạn Thảo đã nói.
b) So sánh \(AB + BC\)và AC.
Phương pháp giải:
a) Học sinh sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC.
b) Dựa vào độ dài của các cạnh để so sánh \(AB + BC\) và AC.
Lời giải chi tiết:
a) Bạn Thảo nói đúng.
b) \(AB + BC = 3 + 2 = 5 > AC = 4\).
Vậy \(AB + BC\) > AC.
Cho tam giác ABC có \(AB = 2\)cm, \(BC = 4\)cm. So sánh hai cạnh AC và AB.
Phương pháp giải:
Trong một tam giác, hiệu độ dài hai cạnh bất kì luôn nhỏ hơn độ dài cạnh còn lại.
Lời giải chi tiết:
Ta có: \(BC - AB = 4 - 2 = 2\).
Mà AC > BC - AB nên độ dài cạnh AC lớn hơn 2 hay AC > AB (vì \(AB = 2\)cm).
Mục II trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải toán. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để đơn giản hóa biểu thức, tìm giá trị của biểu thức, và giải các bài toán thực tế.
Bài tập 1 yêu cầu học sinh điền vào chỗ trống để hoàn thiện các đẳng thức đại số. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép cộng, trừ, nhân, chia đa thức, và các hằng đẳng thức đại số cơ bản.
Ví dụ:
Bài tập 2 yêu cầu học sinh thu gọn biểu thức đại số. Để giải bài tập này, học sinh cần thực hiện các phép toán cộng, trừ, nhân, chia các đơn thức đồng dạng, và sử dụng các quy tắc về dấu ngoặc.
Ví dụ:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Bài tập 3 yêu cầu học sinh tìm giá trị của biểu thức đại số khi biết giá trị của các biến. Để giải bài tập này, học sinh cần thay các giá trị đã cho vào biểu thức và thực hiện các phép toán để tính ra kết quả.
Ví dụ:
Cho x = 2 và y = -1. Tính giá trị của biểu thức A = 2x + 3y.
A = 2 * 2 + 3 * (-1) = 4 - 3 = 1
Bài tập 4 thường là các bài toán ứng dụng, yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các vấn đề thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các yếu tố quan trọng, và xây dựng phương trình hoặc biểu thức đại số phù hợp.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 7:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải các bài tập trong mục II trang 75, 76 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!