Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục III trang 84, 85 SGK Toán 7 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Bài tập mục III tập trung vào các kiến thức về... (phần này sẽ được điền đầy đủ trong bài viết descript_end)
Nêu công thức tính thể tích hình hộp chữ nhật ABCD.A’B’C’D’.
Nêu công thức tính thể tích hình hộp chữ nhật ABCD.A’B’C’D’.
Phương pháp giải:
Công thức tính thể tích hình hộp chữ nhật
Lời giải chi tiết:
Công thức tính thể tích hình hộp chữ nhật là: S.h với S là diện tích đáy; h là chiều cao của hình hộp
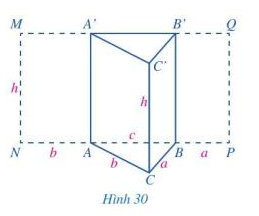
Quan sát hình lăng trụ đứng tam giác (Hình 30). Trải mặt bên AA’C’C thành hình chữ nhật AA’MN. Trải mặt bên BB’C’C thành hình chữ nhật BB’QP.
a) Tính diện tích hình chữ nhật MNPQ
b) So sánh diện tích của hình chữ nhật MNPQ với tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó.
c) So sánh diện tích của hình chữ nhật MNPQ với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Tính và so sánh
Lời giải chi tiết:
a) Diện tích hình chữ nhật MNPQ là: S = MN . NP = h.(b+c+a)
b) Chu vi đáy của hình lăng trụ tam giác là: CABC = a+b+c
Tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó là:
(a+b+c).h
Như vậy, diện tích của hình chữ nhật MNPQ bằng tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó
c) Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’ là: Sxq = SABB’A’ + SACC’A’ + SBCC’B’ = h.c+h.b+h.a = h.(c+b+a)
Vậy diện tích của hình chữ nhật MNPQ bằng diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Nêu công thức tính thể tích hình hộp chữ nhật ABCD.A’B’C’D’.
Phương pháp giải:
Công thức tính thể tích hình hộp chữ nhật
Lời giải chi tiết:
Công thức tính thể tích hình hộp chữ nhật là: S.h với S là diện tích đáy; h là chiều cao của hình hộp
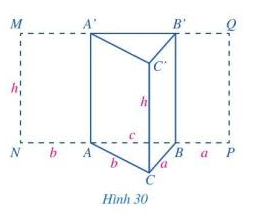
Quan sát hình lăng trụ đứng tam giác (Hình 30). Trải mặt bên AA’C’C thành hình chữ nhật AA’MN. Trải mặt bên BB’C’C thành hình chữ nhật BB’QP.
a) Tính diện tích hình chữ nhật MNPQ
b) So sánh diện tích của hình chữ nhật MNPQ với tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó.
c) So sánh diện tích của hình chữ nhật MNPQ với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Tính và so sánh
Lời giải chi tiết:
a) Diện tích hình chữ nhật MNPQ là: S = MN . NP = h.(b+c+a)
b) Chu vi đáy của hình lăng trụ tam giác là: CABC = a+b+c
Tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó là:
(a+b+c).h
Như vậy, diện tích của hình chữ nhật MNPQ bằng tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó
c) Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’ là: Sxq = SABB’A’ + SACC’A’ + SBCC’B’ = h.c+h.b+h.a = h.(c+b+a)
Vậy diện tích của hình chữ nhật MNPQ bằng diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Mục III trong SGK Toán 7 tập 1 - Cánh diều thường xoay quanh các chủ đề về số nguyên, các phép toán trên số nguyên, và các tính chất cơ bản của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục III trang 84 và 85, giúp các em học sinh hiểu rõ cách giải và áp dụng vào các bài tập tương tự.
Bài tập 1 thường yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số nguyên. Để giải bài tập này, các em cần nắm vững quy tắc dấu trong các phép toán:
Ví dụ: Tính (-5) + 3 = -2
Bài tập 2 có thể yêu cầu học sinh tìm số nguyên thỏa mãn một điều kiện nào đó. Để giải bài tập này, các em cần sử dụng các kiến thức về bất đẳng thức và các phép toán trên số nguyên.
Ví dụ: Tìm số nguyên x thỏa mãn x + 5 > 2
Giải: x + 5 > 2 => x > 2 - 5 => x > -3
Bài tập 3 thường liên quan đến việc áp dụng các tính chất của phép cộng, phép nhân để tính toán nhanh chóng và hiệu quả.
Ví dụ: Tính nhanh: 123 + (-45) + 67 + (-89)
Giải: 123 + (-45) + 67 + (-89) = (123 + 67) + (-45 - 89) = 190 + (-134) = 56
Bài tập 4 có thể là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về số nguyên để giải quyết. Việc đọc kỹ đề bài và xác định đúng các yếu tố liên quan là rất quan trọng.
Ví dụ: Một người nông dân có 5000 đồng. Anh ta mua 3 kg gạo với giá 15000 đồng/kg. Hỏi anh ta còn lại bao nhiêu tiền?
Giải: Số tiền mua gạo là: 3 * 15000 = 45000 đồng. Số tiền còn lại là: 5000 - 45000 = -40000 đồng. (Lưu ý: Kết quả âm có nghĩa là người nông dân còn nợ tiền)
Ngoài SGK Toán 7 tập 1 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập mục III trang 84, 85 SGK Toán 7 tập 1 - Cánh diều. Chúc các em học tập tốt!