Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 74 và 75 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
I. Quan hệ giữa góc và cạnh đối diện trong một tam giác
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Phương pháp giải:
Góc lớn nhất trong tam giác là góc đối diện với cạnh lớn nhất trong tam giác.
Góc nhỏ nhất trong tam giác là góc đối diện với cạnh nhỏ nhất trong tam giác.
Lời giải chi tiết:
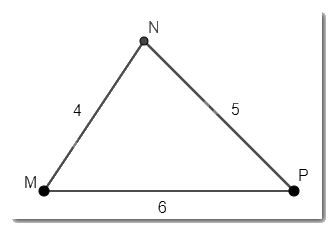
Trong tam giác MNP:\(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
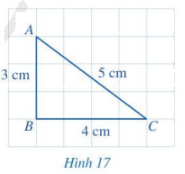
Quan sát tam giác ABC ở Hình 17.
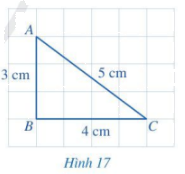
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
Phương pháp giải:
a) Dựa vào độ dài cạnh đã cho để so sánh hai cạnh AB và AC.
b) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
Lời giải chi tiết:
a) Trong tam giác ABC:
\(AB = 3\) cm, \(AC = 5\) cm.
Vậy AB < AC.
b) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
Quan sát tam giác ABC ở Hình 19.
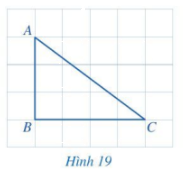
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
Phương pháp giải:
a) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
b) Học sinh có thể dùng thước kẻ (có chia vạch đo) để so sánh hai cạnh hoặc dựa vào độ dài được kẻ của các cạnh trên hình (mỗi một cạnh ô vuông là 1 cm).
Lời giải chi tiết:
a) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
b) Ta có: \(AB = 3\)cm, \(AC = 5\) cm. Vậy AB < AC.
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Phương pháp giải:
a) So sánh hai góc đối diện với hai cạnh để so sánh hai cạnh. (Góc đối diện với cạnh lớn hơn thì cạnh lớn hơn)
b) Cạnh nhỏ nhất trong tam giác là cạnh đối diện với góc nhỏ nhất trong tam giác.
Cạnh lớn nhất trong tam giác là cạnh đối diện với góc lớn nhất trong tam giác.
Lời giải chi tiết:
a)
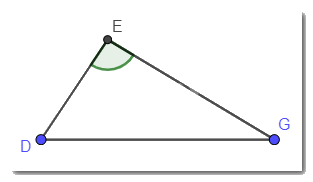
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)
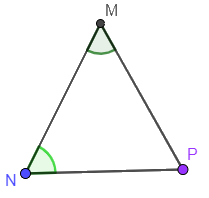
Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
I. Quan hệ giữa góc và cạnh đối diện trong một tam giác
Quan sát tam giác ABC ở Hình 17.
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
Phương pháp giải:
a) Dựa vào độ dài cạnh đã cho để so sánh hai cạnh AB và AC.
b) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
Lời giải chi tiết:
a) Trong tam giác ABC:
\(AB = 3\) cm, \(AC = 5\) cm.
Vậy AB < AC.
b) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Phương pháp giải:
Góc lớn nhất trong tam giác là góc đối diện với cạnh lớn nhất trong tam giác.
Góc nhỏ nhất trong tam giác là góc đối diện với cạnh nhỏ nhất trong tam giác.
Lời giải chi tiết:
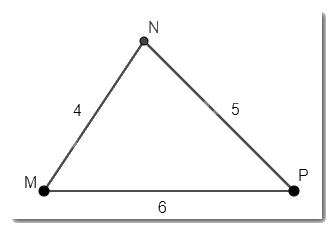
Trong tam giác MNP:\(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
Quan sát tam giác ABC ở Hình 19.
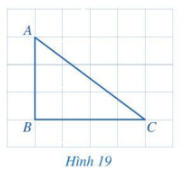
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
Phương pháp giải:
a) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
b) Học sinh có thể dùng thước kẻ (có chia vạch đo) để so sánh hai cạnh hoặc dựa vào độ dài được kẻ của các cạnh trên hình (mỗi một cạnh ô vuông là 1 cm).
Lời giải chi tiết:
a) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
b) Ta có: \(AB = 3\)cm, \(AC = 5\) cm. Vậy AB < AC.
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Phương pháp giải:
a) So sánh hai góc đối diện với hai cạnh để so sánh hai cạnh. (Góc đối diện với cạnh lớn hơn thì cạnh lớn hơn)
b) Cạnh nhỏ nhất trong tam giác là cạnh đối diện với góc nhỏ nhất trong tam giác.
Cạnh lớn nhất trong tam giác là cạnh đối diện với góc lớn nhất trong tam giác.
Lời giải chi tiết:
a)
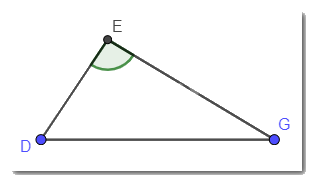
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)
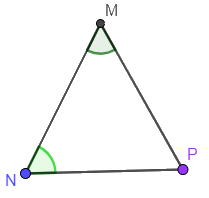
Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
Mục I trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, đơn thức, đa thức. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng biến đổi biểu thức, thực hiện các phép toán với đơn thức và đa thức, đồng thời áp dụng kiến thức vào giải các bài toán thực tế.
Bài tập này yêu cầu học sinh nhắc lại các khái niệm cơ bản về biểu thức đại số, các loại biểu thức đại số, và cách xác định giá trị của biểu thức đại số khi biết giá trị của các biến.
Bài tập này tập trung vào việc ôn tập các khái niệm về đơn thức, bậc của đơn thức, và các phép toán với đơn thức (cộng, trừ, nhân, chia).
Bài tập này yêu cầu học sinh ôn tập các khái niệm về đa thức, bậc của đa thức, và các phép toán với đa thức (cộng, trừ, nhân, chia).
Ví dụ 3: Tìm bậc của đa thức P(x) = 2x3 - 5x2 + x - 1.
Hướng dẫn: Bậc của đa thức là bậc cao nhất của các hạng tử trong đa thức. Trong đa thức P(x), bậc cao nhất là 3, vậy bậc của đa thức là 3.
Các bài tập thực hành trong mục I trang 74, 75 SGK Toán 7 tập 2 - Cánh diều được thiết kế để giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Các bài tập này bao gồm nhiều dạng khác nhau, từ các bài tập đơn giản đến các bài tập phức tạp hơn.
| Công thức | Mô tả |
|---|---|
| A + B = B + A | Tính chất giao hoán của phép cộng |
| (A + B) + C = A + (B + C) | Tính chất kết hợp của phép cộng |
| A * B = B * A | Tính chất giao hoán của phép nhân |
| (A * B) * C = A * (B * C) | Tính chất kết hợp của phép nhân |
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục I trang 74, 75 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt!