Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 103 SGK Toán 7 tập 2 - Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải bài tập, nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.
Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:
Đề bài
Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:
a) \(MB = AI + IM\);
b) MA < MB.
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực thì cách đều hai đầu mút.
b) Dựa vào tính chất trong tam giác: Tổng hai cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
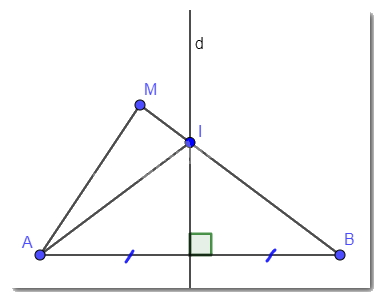
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).
Bài 4 trang 103 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về tam giác cân, tính chất đường trung tuyến trong tam giác, và các định lý liên quan đến góc trong tam giác. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp chứng minh hình học.
Bài 4 yêu cầu học sinh chứng minh một số tính chất liên quan đến tam giác cân và đường trung tuyến. Cụ thể, bài toán thường yêu cầu chứng minh:
Để giải bài toán này, học sinh có thể áp dụng các phương pháp sau:
a) Chứng minh nếu tam giác ABC cân tại A, đường trung tuyến AM thì AM là đường cao và AM là đường phân giác.
Chứng minh:
b) Chứng minh nếu tam giác ABC có đường trung tuyến AM đồng thời là đường cao thì tam giác ABC cân tại A.
Chứng minh:
Để củng cố kiến thức về bài 4 trang 103 SGK Toán 7 tập 2 - Cánh diều, các em có thể tự giải các bài tập sau:
Bài 4 trang 103 SGK Toán 7 tập 2 - Cánh diều là một bài toán quan trọng giúp học sinh hiểu rõ hơn về tính chất của tam giác cân và đường trung tuyến. Việc nắm vững phương pháp giải bài toán này sẽ giúp các em tự tin hơn trong quá trình học tập môn Toán.