Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong Mục I trang 84 và 85 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
I. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.
Phương pháp giải:
Muốn chứng minh MP = NP, ta chứng minh tam giác MOP bằng tam giác NOP.
Lời giải chi tiết:
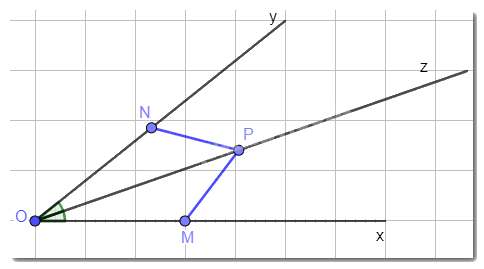
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)
Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.
Phương pháp giải:
Chứng minh tam giác OMQ bằng tam giác OPN. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết:
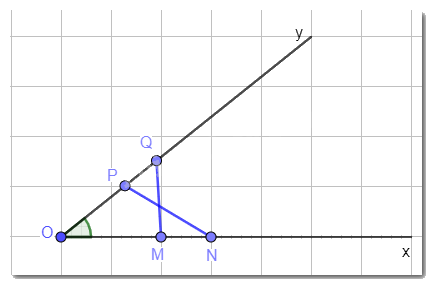
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.
Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)
\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
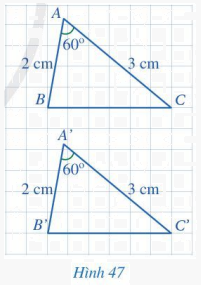
Phương pháp giải:
Đếm số ô vuông rồi so sánh BC và B’C’. Từ đó so sánh hai tam giác ABC và A’B’C’.
Lời giải chi tiết:
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
I. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
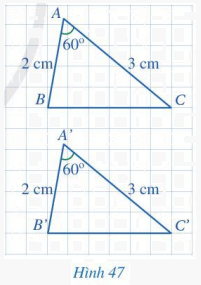
Phương pháp giải:
Đếm số ô vuông rồi so sánh BC và B’C’. Từ đó so sánh hai tam giác ABC và A’B’C’.
Lời giải chi tiết:
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.
Phương pháp giải:
Chứng minh tam giác OMQ bằng tam giác OPN. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết:
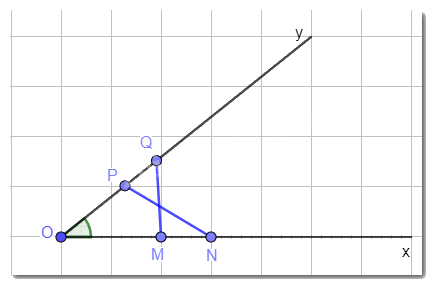
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.
Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)
\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.
Phương pháp giải:
Muốn chứng minh MP = NP, ta chứng minh tam giác MOP bằng tam giác NOP.
Lời giải chi tiết:
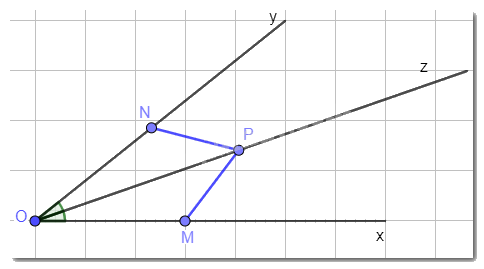
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)
Mục I trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tam giác, các trường hợp bằng nhau của tam giác, và các tính chất liên quan đến góc trong tam giác. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 yêu cầu học sinh ôn lại các khái niệm cơ bản về tam giác: định nghĩa, các loại tam giác (tam giác đều, tam giác cân, tam giác vuông), các yếu tố của tam giác (cạnh, góc). Đồng thời, bài tập cũng giúp học sinh rèn luyện kỹ năng vẽ tam giác theo các điều kiện cho trước.
Đây là phần quan trọng nhất của Mục I. Học sinh cần nắm vững ba trường hợp bằng nhau của tam giác: cạnh - cạnh - cạnh (c-c-c), cạnh - góc - cạnh (c-g-c), góc - cạnh - góc (g-c-g). Bài tập trong phần này yêu cầu học sinh vận dụng các trường hợp bằng nhau để chứng minh hai tam giác bằng nhau, từ đó suy ra các yếu tố tương ứng bằng nhau.
Bài 3 giới thiệu về các điểm đồng quy của tam giác: trọng tâm, trực tâm, đường trung tuyến, đường cao, đường phân giác. Học sinh cần hiểu rõ định nghĩa, tính chất và cách xác định các điểm này. Bài tập yêu cầu học sinh vận dụng các tính chất để giải các bài toán liên quan đến các điểm đồng quy.
Ngoài SGK Toán 7 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong Mục I trang 84, 85 SGK Toán 7 tập 2 - Cánh diều, các em sẽ học tốt môn Toán và đạt kết quả cao trong học tập. Chúc các em thành công!