Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của trang web giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 7 Cánh Diều, đặc biệt là các bài tập trang 70, 71 và 72.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b). Quan sát Hình 2b và dự đoán tổng ba góc A, B, C.
Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó.
Phương pháp giải:
Tổng ba góc trong một tam giác bằng 180°.
Đặc điểm của tam giác đều: độ dài các cạnh bằng nhau, các góc có số đo bằng nhau.
Lời giải chi tiết:
Số đo mỗi góc của tam giác đều bằng \(\dfrac{{180}}{3} = 60^\circ \).
Cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b). Quan sát Hình 2b và dự đoán tổng ba góc A, B, C.
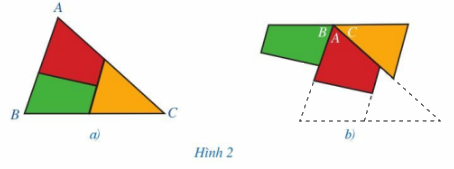
Phương pháp giải:
Số góc của bẹt là \(180^\circ \).
Lời giải chi tiết:
Dự đoán tổng ba góc: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Trong bài toán nêu ở phần mở đầu, hãy tính độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang.
Phương pháp giải:
Xác định đâu là góc (độ nghiêng) tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất).
Lời giải chi tiết:

Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).
Ta có:
\(\widehat B + 90^\circ + 18^\circ = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra: \(\widehat B = 180^\circ - 90^\circ - 18^\circ = 72^\circ \)
Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là 72°.
Cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b). Quan sát Hình 2b và dự đoán tổng ba góc A, B, C.
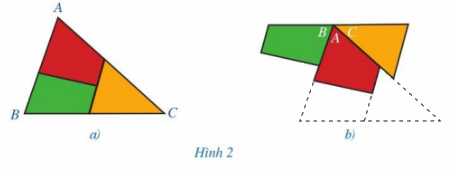
Phương pháp giải:
Số góc của bẹt là \(180^\circ \).
Lời giải chi tiết:
Dự đoán tổng ba góc: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó.
Phương pháp giải:
Tổng ba góc trong một tam giác bằng 180°.
Đặc điểm của tam giác đều: độ dài các cạnh bằng nhau, các góc có số đo bằng nhau.
Lời giải chi tiết:
Số đo mỗi góc của tam giác đều bằng \(\dfrac{{180}}{3} = 60^\circ \).
Trong bài toán nêu ở phần mở đầu, hãy tính độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang.
Phương pháp giải:
Xác định đâu là góc (độ nghiêng) tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất).
Lời giải chi tiết:

Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).
Ta có:
\(\widehat B + 90^\circ + 18^\circ = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra: \(\widehat B = 180^\circ - 90^\circ - 18^\circ = 72^\circ \)
Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là 72°.
Chương trình Toán 7 tập 2 Cánh Diều tập trung vào các chủ đề quan trọng như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và hệ phương trình bậc nhất một ẩn. Việc nắm vững kiến thức và kỹ năng giải toán trong chương trình này là nền tảng vững chắc cho các em học sinh tiếp tục học tập ở các lớp trên.
Trang 70 SGK Toán 7 tập 2 Cánh Diều là phần ôn tập chương 3, bao gồm các bài tập tổng hợp về biểu thức đại số. Các bài tập này giúp các em củng cố kiến thức về các phép toán với biểu thức đại số, rút gọn biểu thức và tìm giá trị của biểu thức.
Trang 71 tiếp tục phần ôn tập chương 3 với các bài tập về phân tích đa thức thành nhân tử. Đây là một kỹ năng quan trọng trong việc giải các bài toán đại số.
Trang 72 SGK Toán 7 tập 2 Cánh Diều bắt đầu phần ôn tập chương 4, tập trung vào phương trình bậc nhất một ẩn. Các bài tập này giúp các em ôn lại các kiến thức về phương trình, cách giải phương trình và ứng dụng của phương trình trong giải toán.
| Bài | Nội dung |
|---|---|
| Bài 7 | Giải phương trình: 2x + 3 = 7 |
| Bài 8 | Giải phương trình: 5x - 10 = 0 |
| Bài 9 | Tìm x biết: 3(x - 1) = 6 |
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết cho từng bài tập, kèm theo phương pháp giải rõ ràng và dễ hiểu. Các em có thể tham khảo lời giải để hiểu rõ hơn về cách giải toán và áp dụng vào các bài tập tương tự.
Khi giải bài tập Toán 7, các em cần lưu ý một số điều sau:
Hy vọng với những lời giải chi tiết và phương pháp giải rõ ràng tại giaitoan.edu.vn, các em sẽ học tập tốt môn Toán 7 và đạt kết quả cao trong học tập.