Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 101 và 102 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
II. Tính chất
Cho đoạn thẳng ABcó trung điểmO. Giả sử M là một điểm khác O sao cho MA = MB.
a) Hai tam giác\(\Delta MOA\) và \(\Delta MOB\) có bằng nhau hay không? Vì sao?
b) Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?
Phương pháp giải:
a) Chứng minh hai tam giác MOA và MOB bằng nhau theo trường hợp c.c.c.
b) Để xem MO có là đường trung trực của AB hay không, ta tìm mối liên hệ giữa MO và AB.
Lời giải chi tiết:
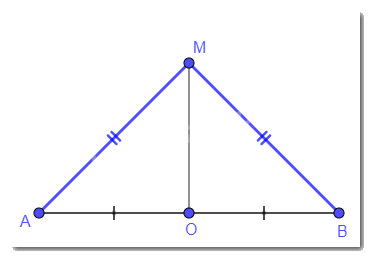
a) Xét hai tam giác MOA và MOB có:
OA = OB (O là trung điểm của AB);
MO chung;
MA = MB.
Vậy \(\Delta MOA = \Delta MOB\)(c.c.c).
b) \(\Delta MOA = \Delta MOB\)nên \(\widehat {MOA} = \widehat {MOB} = \dfrac{1}{2}\widehat {AOB} = 90^\circ \)hay \(MO \bot AB\).
Vậy MO có là đường trung trực của đoạn thẳng AB (MO đi qua trung điểm O của đoạn thẳng AB và vuông góc với đoạn thẳng AB).
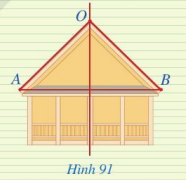
Hình 91 mô tả mặt cắt đứng của một ngôi nhà với hai mái là OA và OB, mái nhà bên trái dài 3 m. Tính chiều dài mái nhà bên phải, biết rằng điểm O thuộc đường trung trực của đoạn thẳng AB.
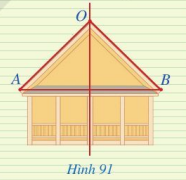
Phương pháp giải:
Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Lời giải chi tiết:
O thuộc đường trung trực của đoạn thẳng AB nên OA = OB (tính chất đường trung trực của đoạn thẳng).
Vậy suy ra mái nhà bên trái dài 3 m nên mái nhà bên phải cũng dài 3 m.
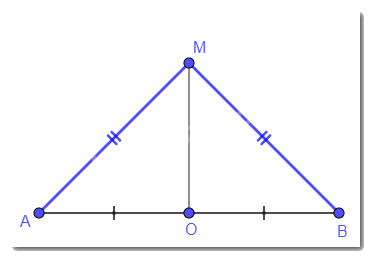
Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d,M khác O(Hình 90).
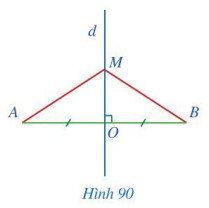
Chứng minh rằng:
a) \(\Delta MOA = \Delta MOB\);
b) MA = MB.
Phương pháp giải:
a) Chứng minh \(\Delta MOA = \Delta MOB\)theo trường hợp c.g.c.
b) Dựa vào kết quả của phần a) để chứng minh MA = MB.
Lời giải chi tiết:
a)Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)
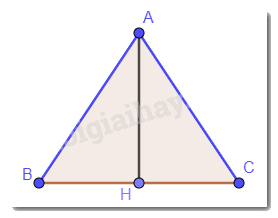
Cho tam giác ABC cân tại A.
a) Điểm A có thuộc đường trung trực của đoạn thẳng BC hay không? Vì sao?
b) Đường thẳng qua A vuông góc với BC cắt cạnh BC tại H. Đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không? Vì sao?
Phương pháp giải:
a) Dựa vào tính chất của đường thẳng trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường thẳng trung trực của đoạn thẳng đó.
b) Muốn xem đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không, ta tìm mối liên hệ giữa AH với đoạn thẳng BC.
Lời giải chi tiết:
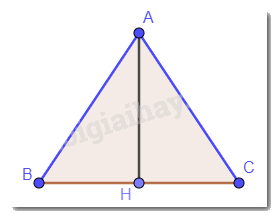
a) Tam giác ABC cân tại A nên AB = AC. Vậy điểm A có thuộc đường trung trực của đoạn thẳng BC.
b) Ta có tam giác ABC cân mà đường thẳng qua A vuông góc với BC cắt BC tại H nên H là trung điểm của BC.
Vậy AH là đường trung trực của đoạn thẳng BC. (AH đi qua trung điểm H của đoạn thẳng BC và vuông góc với đoạn thẳng BC).
II. Tính chất
Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d,M khác O(Hình 90).

Chứng minh rằng:
a) \(\Delta MOA = \Delta MOB\);
b) MA = MB.
Phương pháp giải:
a) Chứng minh \(\Delta MOA = \Delta MOB\)theo trường hợp c.g.c.
b) Dựa vào kết quả của phần a) để chứng minh MA = MB.
Lời giải chi tiết:
a)Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)
Hình 91 mô tả mặt cắt đứng của một ngôi nhà với hai mái là OA và OB, mái nhà bên trái dài 3 m. Tính chiều dài mái nhà bên phải, biết rằng điểm O thuộc đường trung trực của đoạn thẳng AB.
Phương pháp giải:
Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Lời giải chi tiết:
O thuộc đường trung trực của đoạn thẳng AB nên OA = OB (tính chất đường trung trực của đoạn thẳng).
Vậy suy ra mái nhà bên trái dài 3 m nên mái nhà bên phải cũng dài 3 m.
Cho đoạn thẳng ABcó trung điểmO. Giả sử M là một điểm khác O sao cho MA = MB.
a) Hai tam giác\(\Delta MOA\) và \(\Delta MOB\) có bằng nhau hay không? Vì sao?
b) Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?
Phương pháp giải:
a) Chứng minh hai tam giác MOA và MOB bằng nhau theo trường hợp c.c.c.
b) Để xem MO có là đường trung trực của AB hay không, ta tìm mối liên hệ giữa MO và AB.
Lời giải chi tiết:
a) Xét hai tam giác MOA và MOB có:
OA = OB (O là trung điểm của AB);
MO chung;
MA = MB.
Vậy \(\Delta MOA = \Delta MOB\)(c.c.c).
b) \(\Delta MOA = \Delta MOB\)nên \(\widehat {MOA} = \widehat {MOB} = \dfrac{1}{2}\widehat {AOB} = 90^\circ \)hay \(MO \bot AB\).
Vậy MO có là đường trung trực của đoạn thẳng AB (MO đi qua trung điểm O của đoạn thẳng AB và vuông góc với đoạn thẳng AB).
Cho tam giác ABC cân tại A.
a) Điểm A có thuộc đường trung trực của đoạn thẳng BC hay không? Vì sao?
b) Đường thẳng qua A vuông góc với BC cắt cạnh BC tại H. Đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không? Vì sao?
Phương pháp giải:
a) Dựa vào tính chất của đường thẳng trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường thẳng trung trực của đoạn thẳng đó.
b) Muốn xem đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không, ta tìm mối liên hệ giữa AH với đoạn thẳng BC.
Lời giải chi tiết:
a) Tam giác ABC cân tại A nên AB = AC. Vậy điểm A có thuộc đường trung trực của đoạn thẳng BC.
b) Ta có tam giác ABC cân mà đường thẳng qua A vuông góc với BC cắt BC tại H nên H là trung điểm của BC.
Vậy AH là đường trung trực của đoạn thẳng BC. (AH đi qua trung điểm H của đoạn thẳng BC và vuông góc với đoạn thẳng BC).
Mục II trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức đã học về tam giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tam giác, đặc biệt là các bài toán về tổng ba góc trong một tam giác, quan hệ giữa góc và cạnh đối diện trong tam giác.
Bài 1 thường là các bài tập trắc nghiệm hoặc điền vào chỗ trống để kiểm tra kiến thức cơ bản về tam giác. Các em cần nắm vững các khái niệm như tam giác là gì, các loại tam giác (tam giác đều, tam giác cân, tam giác vuông), các yếu tố của tam giác (góc, cạnh).
Bài 2 yêu cầu học sinh tính góc còn lại của một tam giác khi biết hai góc. Để giải bài này, các em cần nhớ định lý về tổng ba góc trong một tam giác: tổng ba góc trong một tam giác bằng 180 độ.
Ví dụ:
Bài 3 thường yêu cầu học sinh so sánh độ dài các cạnh của một tam giác dựa vào số đo các góc đối diện. Các em cần nhớ quy tắc: trong một tam giác, cạnh lớn hơn đối diện với góc lớn hơn.
Ví dụ:
Cho tam giác ABC có góc B > góc C. So sánh các cạnh AB và AC.
Giải: Vì góc B > góc C nên AB > AC.
Bài 4 thường là các bài tập phức tạp hơn, yêu cầu học sinh vận dụng kết hợp nhiều kiến thức và kỹ năng đã học để giải quyết. Các bài tập này thường liên quan đến việc chứng minh các tính chất hình học, giải các bài toán thực tế.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục II trang 101, 102 SGK Toán 7 tập 2 - Cánh diều, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập. Các lời giải này sẽ được trình bày một cách rõ ràng, dễ hiểu, kèm theo các hình vẽ minh họa (nếu cần thiết).
Ngoài SGK Toán 7 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải bài tập trong bài viết này, các em sẽ tự tin hơn trong việc học tập môn Toán 7. Chúc các em học tốt!