Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 65 và 66 sách giáo khoa Toán 7 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau:
Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau:
x | x1 = 20 | x2 = 18 | x3 = 15 | x4 = 5 |
y | y1 = 9 | y2 = ? | y3 = ? | y4 = ? |
a) Hãy xác định hệ số tỉ lệ
b) Tìm số thích hợp cho ? trong bảng trên
c) So sánh các tỉ số: x1y1 ; x2y2 ; x3y3 ; x4y4.
d) So sánh các tỉ số: \(\frac{{{x_1}}}{{{x_2}}}\) và \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\) và \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) và \(\frac{{{y_4}}}{{{y_3}}}\)
Phương pháp giải:
+ Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay x.y = a (a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a
+ Tính các tích rồi so sánh
+ Tính các tỉ số rồi so sánh
Lời giải chi tiết:
a) Hệ số tỉ lệ a = x1.y1 = 20. 9 =180
b) Ta có: y= \(\frac{{180}}{x}\)
Khi x2 = 18 thì y2 = \(\frac{{180}}{{{x_2}}} = \frac{{180}}{{18}} = 10\)
Khi x3 = 15 thì y3 = \(\frac{{180}}{{{x_3}}} = \frac{{180}}{{15}} = 12\)
Khi x4 = 18 thì y4 = \(\frac{{180}}{{{x_4}}} = \frac{{180}}{5} = 36\)
c) Tích x1.y1 = 20. 9 =180
x2.y2 = 18.10 =180
x3.y3 = 15.12 =180
x4.y4 = 5.36 =180
Vậy x1y1 = x2y2 = x3y3 = x4y4 =180
d) Ta có:
\(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{20}}{{18}}\)=\(\frac{{10}}{9}\) ; \(\frac{{{y_2}}}{{{y_1}}}\)= \(\frac{{10}}{9}\)
\(\frac{{{x_1}}}{{{x_3}}}\) = \(\frac{{20}}{{15}}\)=\(\frac{4}{3}\) ; \(\frac{{{y_3}}}{{{y_1}}}\) = \(\frac{{12}}{9}\) = \(\frac{4}{3}\)
\(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{15}}{5}\) = 3; \(\frac{{{y_4}}}{{{y_3}}}\)= \(\frac{{36}}{{12}}\) = 3
Vậy \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\)= \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{{y_4}}}{{{y_3}}}\)
Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau:
x | x1 = 20 | x2 = 18 | x3 = 15 | x4 = 5 |
y | y1 = 9 | y2 = ? | y3 = ? | y4 = ? |
a) Hãy xác định hệ số tỉ lệ
b) Tìm số thích hợp cho ? trong bảng trên
c) So sánh các tỉ số: x1y1 ; x2y2 ; x3y3 ; x4y4.
d) So sánh các tỉ số: \(\frac{{{x_1}}}{{{x_2}}}\) và \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\) và \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) và \(\frac{{{y_4}}}{{{y_3}}}\)
Phương pháp giải:
+ Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay x.y = a (a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a
+ Tính các tích rồi so sánh
+ Tính các tỉ số rồi so sánh
Lời giải chi tiết:
a) Hệ số tỉ lệ a = x1.y1 = 20. 9 =180
b) Ta có: y= \(\frac{{180}}{x}\)
Khi x2 = 18 thì y2 = \(\frac{{180}}{{{x_2}}} = \frac{{180}}{{18}} = 10\)
Khi x3 = 15 thì y3 = \(\frac{{180}}{{{x_3}}} = \frac{{180}}{{15}} = 12\)
Khi x4 = 18 thì y4 = \(\frac{{180}}{{{x_4}}} = \frac{{180}}{5} = 36\)
c) Tích x1.y1 = 20. 9 =180
x2.y2 = 18.10 =180
x3.y3 = 15.12 =180
x4.y4 = 5.36 =180
Vậy x1y1 = x2y2 = x3y3 = x4y4 =180
d) Ta có:
\(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{20}}{{18}}\)=\(\frac{{10}}{9}\) ; \(\frac{{{y_2}}}{{{y_1}}}\)= \(\frac{{10}}{9}\)
\(\frac{{{x_1}}}{{{x_3}}}\) = \(\frac{{20}}{{15}}\)=\(\frac{4}{3}\) ; \(\frac{{{y_3}}}{{{y_1}}}\) = \(\frac{{12}}{9}\) = \(\frac{4}{3}\)
\(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{15}}{5}\) = 3; \(\frac{{{y_4}}}{{{y_3}}}\)= \(\frac{{36}}{{12}}\) = 3
Vậy \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\)= \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{{y_4}}}{{{y_3}}}\)
Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp \(\frac{4}{3}\) vận tốc dự định. Tính thời gian ô tô đã đi.
Phương pháp giải:
Thời gian ô tô đi và vận tốc đi trên cùng 1 quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\)
Lời giải chi tiết:
Vì v. t = s không đổi nên vận tốc và thời gian ô tô đi là 2 đại lượng tỉ lệ nghịch
Theo tính chất 2 đại lượng tỉ lệ nghịch, ta có:
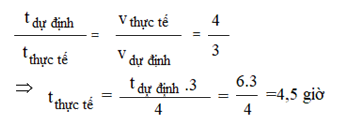
Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp \(\frac{4}{3}\) vận tốc dự định. Tính thời gian ô tô đã đi.
Phương pháp giải:
Thời gian ô tô đi và vận tốc đi trên cùng 1 quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\)
Lời giải chi tiết:
Vì v. t = s không đổi nên vận tốc và thời gian ô tô đi là 2 đại lượng tỉ lệ nghịch
Theo tính chất 2 đại lượng tỉ lệ nghịch, ta có:
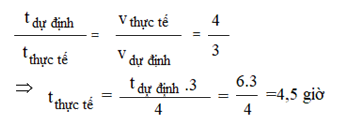
Mục II trong SGK Toán 7 tập 1 - Cánh diều tập trung vào các kiến thức về số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố và ứng dụng của chúng. Việc nắm vững các khái niệm này là nền tảng quan trọng cho các kiến thức toán học nâng cao hơn.
Bài 1 yêu cầu học sinh xác định các số nguyên tố, hợp số trong một dãy số cho trước. Để làm được bài này, học sinh cần hiểu rõ định nghĩa về số nguyên tố (chỉ chia hết cho 1 và chính nó) và hợp số (chia hết cho nhiều số khác ngoài 1 và chính nó).
Bài 2 hướng dẫn học sinh phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố. Đây là một kỹ năng quan trọng trong toán học, giúp học sinh hiểu rõ cấu trúc của các số tự nhiên và ứng dụng trong nhiều bài toán khác.
Ví dụ: Phân tích số 36 ra thừa số nguyên tố:
Bài 3 yêu cầu học sinh sử dụng kiến thức về phân tích ra thừa số nguyên tố để giải các bài toán liên quan đến ước chung, bội chung. Việc hiểu rõ mối liên hệ giữa phân tích ra thừa số nguyên tố và các khái niệm ước, bội sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục II trang 65, 66 SGK Toán 7 tập 1 - Cánh diều:
| Bài tập | Lời giải |
|---|---|
| Bài 1a | ... (Lời giải chi tiết bài 1a) ... |
| Bài 1b | ... (Lời giải chi tiết bài 1b) ... |
| Bài 2a | ... (Lời giải chi tiết bài 2a) ... |
| Bài 2b | ... (Lời giải chi tiết bài 2b) ... |
| Bài 3 | ... (Lời giải chi tiết bài 3) ... |
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 7. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.