Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 111 SGK Toán 7 tập 2 - Cánh diều. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
Đề bài
Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
a) \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \);
b) \(\widehat {BIC} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất của đường phân giác: chia các góc tại các đỉnh thành hai góc bằng nhau.
b) Dựa vào kết quả của phần a).
Lời giải chi tiết
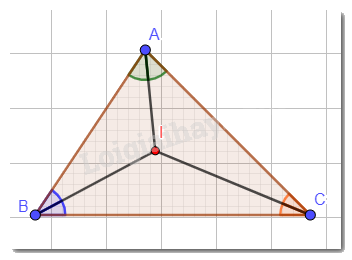
a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
Bài 2 trang 111 SGK Toán 7 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán liên quan đến góc so le trong, góc đồng vị, góc trong cùng phía. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và tính chất sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích từng phần của bài toán. Bài toán thường yêu cầu chúng ta xác định các góc bằng nhau hoặc bù nhau dựa trên các tính chất đã học. Dưới đây là một ví dụ minh họa:
Ví dụ: Cho hình vẽ, biết a // b và góc A1 = 60°. Tính các góc A2, B1, B2.
Giải:
Ngoài dạng bài tập cơ bản như ví dụ trên, bài 2 trang 111 SGK Toán 7 tập 2 - Cánh diều còn có thể xuất hiện các dạng bài tập khác, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Một số dạng bài tập thường gặp bao gồm:
Để nắm vững kiến thức và kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em nên luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, phong phú, giúp các em củng cố kiến thức và nâng cao khả năng giải quyết vấn đề.
Khi giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em nên:
Bài 2 trang 111 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng, giúp các em củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.