Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 90, 91, 92 sách giáo khoa Toán 7 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2. a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB. b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
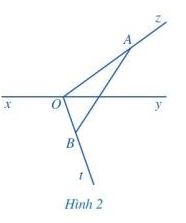
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Phương pháp giải:
Vẽ hình và nhận xét
Lời giải chi tiết:
a)
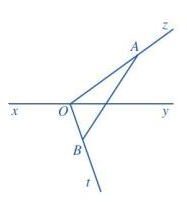
b) Đoạn thẳng AB cắt đường thẳng xy
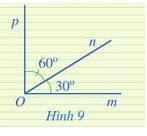
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Tính chất 2 góc kề nhau
Lời giải chi tiết:
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
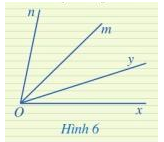
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Lời giải chi tiết:
Hai góc xOy và mOn không phải là hai góc kề nhauvì không có cạnh nào chung.
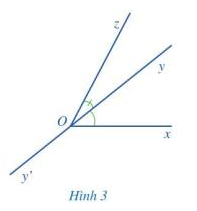
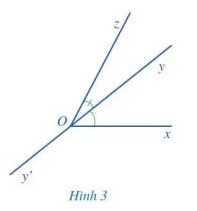
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
+ Vẽ hình và nhận xét
Lời giải chi tiết:
a) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
b)
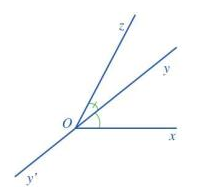
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’
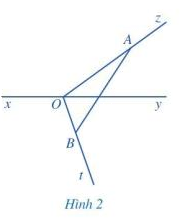
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Phương pháp giải:
Vẽ hình và nhận xét
Lời giải chi tiết:
a)
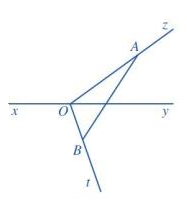
b) Đoạn thẳng AB cắt đường thẳng xy
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
+ Vẽ hình và nhận xét
Lời giải chi tiết:
a) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
b)
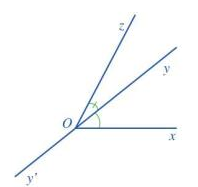
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’
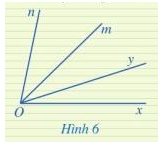
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Lời giải chi tiết:
Hai góc xOy và mOn không phải là hai góc kề nhauvì không có cạnh nào chung.
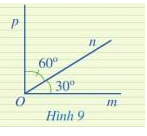
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Tính chất 2 góc kề nhau
Lời giải chi tiết:
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
Mục I trong SGK Toán 7 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa các kiến thức cơ bản về số hữu tỉ, các phép toán trên số hữu tỉ, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 7.
Bài tập này yêu cầu học sinh ôn lại các khái niệm về số hữu tỉ, cách biểu diễn số hữu tỉ trên trục số, và so sánh các số hữu tỉ. Các em cần nắm vững các quy tắc so sánh số hữu tỉ dương, số hữu tỉ âm, và số 0.
Bài tập này tập trung vào việc thực hành các phép cộng, trừ, nhân, chia số hữu tỉ. Các em cần nhớ các quy tắc dấu trong các phép toán này, cũng như các tính chất giao hoán, kết hợp, phân phối của các phép toán.
Bài tập này yêu cầu học sinh vận dụng các tính chất của các phép toán trên số hữu tỉ để giải các bài toán phức tạp hơn. Các em cần rèn luyện kỹ năng biến đổi biểu thức và tìm ra cách giải tối ưu.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục I trang 90, 91, 92 SGK Toán 7 tập 1 - Cánh diều:
Kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ có ứng dụng rất lớn trong đời sống thực tế, ví dụ như:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải các bài tập trong mục I trang 90, 91, 92 SGK Toán 7 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!