Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 108 SGK Toán 7 tập 1 - Cánh diều. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả. Hãy cùng chúng tôi khám phá lời giải chi tiết của bài 5 này nhé!
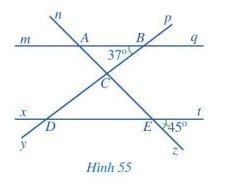
Quan sát Hình 55, trong đó mq // xt a) Kể tên các cặp góc đồng vị bằng nhau. b) Tìm số đo các góc BAC, CDE. c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được
Đề bài
Quan sát Hình 55, trong đó mq // xt
a) Kể tên các cặp góc đồng vị bằng nhau.
b) Tìm số đo các góc BAC, CDE.
c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được \(\widehat {BCE} = 82^\circ \). Theo em, bạn Nam nói đúng hay sai? Vì sao?
Phương pháp giải - Xem chi tiết
+ 2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia Om nằm trong góc xOy thì \(\widehat {xOm} + \widehat {mOy} = \widehat {xOy}\)
Lời giải chi tiết
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
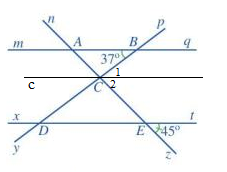
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)
Bài 5 trang 108 SGK Toán 7 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán liên quan đến góc so le trong, góc đồng vị, góc trong cùng phía. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và tính chất sau:
Để giúp các em hiểu rõ hơn về cách giải bài 5 trang 108 SGK Toán 7 tập 1 - Cánh diều, chúng ta sẽ cùng nhau phân tích từng phần của bài tập. Bài tập thường yêu cầu chúng ta xác định các góc so le trong, góc đồng vị, góc trong cùng phía và sử dụng các tính chất để tính toán giá trị của các góc.
Bước đầu tiên là xác định rõ các góc và đường thẳng song song trong hình vẽ. Sử dụng ký hiệu để đánh dấu các góc và đường thẳng, giúp việc phân tích trở nên dễ dàng hơn.
Sau khi xác định được các góc và đường thẳng song song, chúng ta sẽ áp dụng các tính chất của các góc so le trong, góc đồng vị, góc trong cùng phía để thiết lập các phương trình hoặc mối quan hệ giữa các góc.
Giải các phương trình hoặc sử dụng các mối quan hệ đã thiết lập để tìm ra giá trị của các góc cần tính. Lưu ý kiểm tra lại kết quả để đảm bảo tính chính xác.
Giả sử đề bài yêu cầu tính góc x trong hình vẽ, biết rằng đường thẳng a song song với đường thẳng b và góc y = 60 độ. Ta có thể giải bài tập này như sau:
Để củng cố kiến thức và kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em có thể tự giải các bài tập sau:
Để giải bài tập về các góc một cách hiệu quả, các em nên:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết bài 5 trang 108 SGK Toán 7 tập 1 - Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!