Lý thuyết Giá trị tuyệt đối của một số thực Toán 7 Cánh diều

Lý thuyết Giá trị tuyệt đối của một số thực Toán 7 Cánh diều

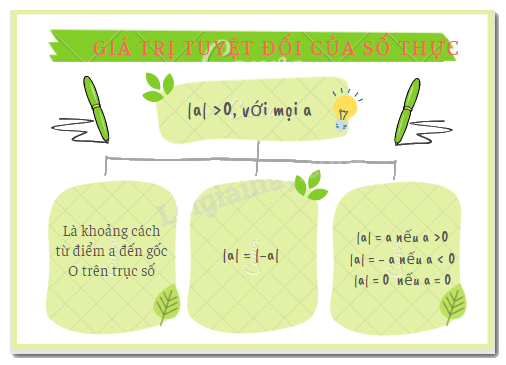
Giá trị tuyệt đối của một số thực là khoảng cách từ số đó đến số 0 trên trục số. Nó được ký hiệu bằng hai dấu gạch đứng bao quanh số đó, ví dụ: |a|.

1. Định nghĩa

Giá trị tuyệt đối của một số thực a, ký hiệu là |a|, được định nghĩa như sau:

• |a| = a nếu a ≥ 0
• |a| = -a nếu a < 0

Ví dụ:

• |5| = 5
• |-3| = 3
• |0| = 0

2. Tính chất của giá trị tuyệt đối

Giá trị tuyệt đối có một số tính chất quan trọng sau:

1. |a| ≥ 0 với mọi số thực a
2. |a| = | -a|
3. |a + b| ≤ |a| + |b| (Bất đẳng thức tam giác)
4. |a - b| ≥ ||a| - |b||
5. |a * b| = |a| * |b|
6. |a / b| = |a| / |b| (với b ≠ 0)

3. Ứng dụng của giá trị tuyệt đối

Giá trị tuyệt đối được sử dụng rộng rãi trong toán học và các lĩnh vực khác, ví dụ:

• Tính khoảng cách giữa hai điểm trên trục số.
• Giải các phương trình và bất phương trình chứa giá trị tuyệt đối.
• Đánh giá sai số trong các phép đo.

4. Bài tập ví dụ

Bài 1: Tính giá trị của biểu thức sau:

|2 - 5| + | -7 + 3| = ?

Giải:

|2 - 5| = |-3| = 3

| -7 + 3| = |-4| = 4

Vậy, |2 - 5| + | -7 + 3| = 3 + 4 = 7

Bài 2: Tìm các giá trị của x thỏa mãn bất phương trình:

|x - 1| ≤ 2

Giải:

Bất phương trình tương đương với:

-2 ≤ x - 1 ≤ 2

Cộng 1 vào cả ba vế, ta được:

-1 ≤ x ≤ 3

Vậy, tập nghiệm của bất phương trình là [-1; 3].

5. Mở rộng kiến thức

Giá trị tuyệt đối còn được mở rộng cho các số phức. Nếu z = a + bi là một số phức, thì giá trị tuyệt đối của z được định nghĩa là:

|z| = √(a² + b²)

6. Luyện tập thêm

Để nắm vững hơn về lý thuyết giá trị tuyệt đối, bạn nên luyện tập thêm nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập này trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.

Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Giá trị tuyệt đối của một số thực Toán 7 Cánh diều. Chúc bạn học tốt!