Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục II trang 64 và 65 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững kiến thức và kỹ năng giải toán, từ đó đạt kết quả tốt nhất trong học tập.
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là
Cho đa thức \(P(x) = 4{x^2} + 3x\) và đơn thức \(Q(x) = 2x\).
a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x).
b) Hãy cộng các thương vừa tìm được.
Phương pháp giải:
a) Để chia từng đơn thức có trong đa thức P(x) cho đơn thức Q(x), trước hết ta phải xác định được các đơn thức có trong đa thức P(x) rồi thực hiện phép tính.
b) Cộng các thương vừa tìm được ở phần a) với nhau.
Lời giải chi tiết:
a) Các đơn thức có trong đa thức P(x) là: \(4{x^2};3x\).
Chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x) được kết quả lần lượt là:
\(4{x^2}:2x = (4:2).({x^2}:x) = 2x\).
\(3x:2x = (3:2).(x:x) = \dfrac{3}{2}\).
b) Cộng các thương vừa tìm được \( = 2x + \dfrac{3}{2}\).
Tính:
\((\dfrac{1}{2}{x^4} - \dfrac{1}{4}{x^3} + x):( - \dfrac{1}{8}x)\).
Phương pháp giải:
Muốn chia đa thức P cho đơn thức Q(Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của P cho đơn thức Q rồi cộng các thương với nhau.
Lời giải chi tiết:
\(\begin{array}{l}(\dfrac{1}{2}{x^4} - \dfrac{1}{4}{x^3} + x):( - \dfrac{1}{8}x) = \dfrac{1}{2}{x^4}:( - \dfrac{1}{8}x) - \dfrac{1}{4}{x^3}:( - \dfrac{1}{8}x) + x:( - \dfrac{1}{8}x)\\ = (\dfrac{1}{2}: - \dfrac{1}{8}).({x^4}:x) - (\dfrac{1}{4}: - \dfrac{1}{8}).({x^3}:x) + (1: - \dfrac{1}{8}).(x:x)\\ = - 4.{x^{4 - 1}} - ( - 2).{x^{3 - 1}} + ( - 8).{x^{1 - 1}}\\ = - 4{x^3} + 2{x^2} - 8\end{array}\)
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là \(A = ac,B = bc\). Biết \(MN = c\).
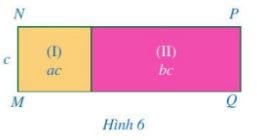
a) Tính NP.
b) So sánh: \((A + B):c\) và \(A:c + B:c\).
Phương pháp giải:
a) NP là độ dài của một cạnh hình chữ nhật. Để tính được NP ta phải tính được diện tích của hình chứa NP. Hoặc tính độ dài của hai cạnh hợp thành NP với diện tích của hình (I), (II) đã cho.
b) Thực hiện hai phép chia \((A + B):c\) và \(A:c + B:c\)rồi so sánh kết quả.
Lời giải chi tiết:
a) Ta có: Diện tích hình chữ nhật MNPQ bằng diện tích hình chữ nhật (I) + diện tích hình chữ nhật (II)
\( = ac + bc = (a + b).c\).
Mà MN = c
Do đó NP = \((a + b).c:c = a + b\).
b) Ta có:
\(\begin{array}{l}(A + B):c = (ac + bc):c = a + b\\A:c + B:c = ac:c + bc:c = a + b\end{array}\)
Vậy \((A + B):c\) =\(A:c + B:c\).
Cho đa thức \(P(x) = 4{x^2} + 3x\) và đơn thức \(Q(x) = 2x\).
a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x).
b) Hãy cộng các thương vừa tìm được.
Phương pháp giải:
a) Để chia từng đơn thức có trong đa thức P(x) cho đơn thức Q(x), trước hết ta phải xác định được các đơn thức có trong đa thức P(x) rồi thực hiện phép tính.
b) Cộng các thương vừa tìm được ở phần a) với nhau.
Lời giải chi tiết:
a) Các đơn thức có trong đa thức P(x) là: \(4{x^2};3x\).
Chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x) được kết quả lần lượt là:
\(4{x^2}:2x = (4:2).({x^2}:x) = 2x\).
\(3x:2x = (3:2).(x:x) = \dfrac{3}{2}\).
b) Cộng các thương vừa tìm được \( = 2x + \dfrac{3}{2}\).
Tính:
\((\dfrac{1}{2}{x^4} - \dfrac{1}{4}{x^3} + x):( - \dfrac{1}{8}x)\).
Phương pháp giải:
Muốn chia đa thức P cho đơn thức Q(Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của P cho đơn thức Q rồi cộng các thương với nhau.
Lời giải chi tiết:
\(\begin{array}{l}(\dfrac{1}{2}{x^4} - \dfrac{1}{4}{x^3} + x):( - \dfrac{1}{8}x) = \dfrac{1}{2}{x^4}:( - \dfrac{1}{8}x) - \dfrac{1}{4}{x^3}:( - \dfrac{1}{8}x) + x:( - \dfrac{1}{8}x)\\ = (\dfrac{1}{2}: - \dfrac{1}{8}).({x^4}:x) - (\dfrac{1}{4}: - \dfrac{1}{8}).({x^3}:x) + (1: - \dfrac{1}{8}).(x:x)\\ = - 4.{x^{4 - 1}} - ( - 2).{x^{3 - 1}} + ( - 8).{x^{1 - 1}}\\ = - 4{x^3} + 2{x^2} - 8\end{array}\)
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là \(A = ac,B = bc\). Biết \(MN = c\).
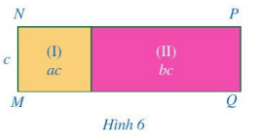
a) Tính NP.
b) So sánh: \((A + B):c\) và \(A:c + B:c\).
Phương pháp giải:
a) NP là độ dài của một cạnh hình chữ nhật. Để tính được NP ta phải tính được diện tích của hình chứa NP. Hoặc tính độ dài của hai cạnh hợp thành NP với diện tích của hình (I), (II) đã cho.
b) Thực hiện hai phép chia \((A + B):c\) và \(A:c + B:c\)rồi so sánh kết quả.
Lời giải chi tiết:
a) Ta có: Diện tích hình chữ nhật MNPQ bằng diện tích hình chữ nhật (I) + diện tích hình chữ nhật (II)
\( = ac + bc = (a + b).c\).
Mà MN = c
Do đó NP = \((a + b).c:c = a + b\).
b) Ta có:
\(\begin{array}{l}(A + B):c = (ac + bc):c = a + b\\A:c + B:c = ac:c + bc:c = a + b\end{array}\)
Vậy \((A + B):c\) =\(A:c + B:c\).
Mục II trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng thu gọn đa thức, tìm bậc của đa thức, và thực hiện các phép cộng, trừ đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học các kiến thức nâng cao hơn về đa thức trong các lớp học tiếp theo.
Bài 1 yêu cầu học sinh thu gọn các đa thức đã cho. Để thu gọn một đa thức, ta cần thực hiện các bước sau:
Ví dụ, để thu gọn đa thức 3x2 + 2x - x2 + 5x, ta thực hiện như sau:
Bài 2 yêu cầu học sinh tìm bậc của các đa thức đã cho. Bậc của một đa thức là bậc cao nhất của các hạng tử trong đa thức đó. Ví dụ, đa thức 2x2 + 7x có bậc là 2.
Để tìm bậc của một đa thức, ta cần thực hiện các bước sau:
Bài 3 yêu cầu học sinh thực hiện các phép cộng, trừ đa thức. Để cộng hoặc trừ hai đa thức, ta cần thực hiện các bước sau:
Ví dụ, để cộng hai đa thức 3x2 + 2x và -x2 + 5x, ta thực hiện như sau:
Khi giải các bài tập về đa thức, học sinh cần lưu ý một số điều sau:
Để học tốt môn Toán, các em nên thường xuyên luyện tập, làm bài tập đầy đủ và tìm hiểu kỹ các kiến thức trong sách giáo khoa. Ngoài ra, các em có thể tham khảo các tài liệu tham khảo, các bài giảng online để mở rộng kiến thức và nâng cao kỹ năng giải toán.
Hy vọng rằng với bài viết này, các em học sinh đã có thể hiểu rõ hơn về cách giải các bài tập trong mục II trang 64, 65 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!