Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 115, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn chinh phục môn Toán một cách hiệu quả.
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Đề bài
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác ABC đều bằng cách chứng minh AB = BC = CA.
Lời giải chi tiết
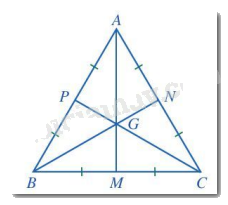
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.
Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.
Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC;BN \bot AC;CP \bot AB\).
Xét tam giác ABM và tam giác ACM có:
AM chung;
\(\widehat {AMB} = \widehat {AMC} (= 90^\circ \))(vì \(AM \bot BC\));
BM = MC (M là trung điểm của BC).
Vậy \(\Delta ABM = \Delta ACM\)(c.g.c). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BNA = \Delta BNC\)(c.g.c). Suy ra: AB = BC( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.
Bài 3 trang 115 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Bài tập yêu cầu học sinh vận dụng kiến thức về các góc để tính toán và chứng minh các mối quan hệ giữa chúng.
Bài 3 gồm các phần nhỏ, mỗi phần yêu cầu học sinh thực hiện một nhiệm vụ cụ thể. Chúng ta sẽ cùng nhau phân tích từng phần:
Ở phần này, học sinh cần quan sát kỹ hình vẽ và xác định các cặp góc đối đỉnh. Góc đối đỉnh là hai góc mà mỗi góc là góc đối của đỉnh của góc kia. Để xác định chính xác, học sinh cần chú ý đến vị trí tương đối của các góc trên hình.
Sau khi đã xác định được các cặp góc đối đỉnh, học sinh có thể sử dụng tính chất của góc đối đỉnh để tính số đo các góc còn lại. Tính chất của góc đối đỉnh là hai góc đối đỉnh thì bằng nhau.
Phần này yêu cầu học sinh vận dụng kiến thức về các góc kề bù để chứng minh một số mối quan hệ giữa các góc. Hai góc kề bù là hai góc có chung một cạnh và tổng số đo của hai góc bằng 180 độ.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin đưa ra hướng dẫn giải chi tiết cho từng phần:
Bước 1: Quan sát hình vẽ và xác định các đỉnh của các góc. Bước 2: Tìm các cặp góc có chung đỉnh và hai cạnh đối nhau. Bước 3: Nêu tên các cặp góc đối đỉnh.
Bước 1: Xác định các góc đối đỉnh với các góc đã biết số đo. Bước 2: Sử dụng tính chất của góc đối đỉnh để tính số đo các góc còn lại. Bước 3: Kiểm tra lại kết quả.
Bước 1: Xác định các góc kề bù. Bước 2: Sử dụng tính chất của góc kề bù để tính số đo các góc. Bước 3: Chứng minh mối quan hệ giữa các góc.
Để củng cố kiến thức đã học, học sinh có thể tự giải các bài tập vận dụng và mở rộng sau:
Bài 3 trang 115 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh nắm vững kiến thức về các góc. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải bài tập và học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!