Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 5 trang 115, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn giải quyết mọi khó khăn trong môn Toán.
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
Đề bài
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất của đường trung trực: đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó.
b) Dựa vào tính chất ba đường trung trực trong tam giác: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Chứng minh \(\widehat {MOB} = \widehat {MOC}\)bằng cách chứng minh tam giác OMB bằng tam giác OMC.
Lời giải chi tiết
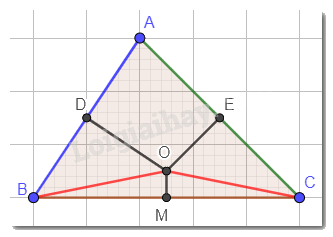
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).
Bài 5 trang 115 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học về các góc và mối quan hệ giữa các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Bài tập 5 yêu cầu học sinh dựa vào hình vẽ và các thông tin đã cho để xác định các góc bằng nhau, các cặp góc so le trong, so le ngoài, đồng vị, trong cùng phía, ngoài cùng phía. Từ đó, suy ra mối quan hệ song song giữa các đường thẳng.
Để giải bài tập này, chúng ta sẽ tiến hành theo các bước sau:
Giả sử, cho hình vẽ với hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc A1 = 60 độ. Hãy tìm các góc bằng nhau và suy ra mối quan hệ song song giữa a và b.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về các góc và đường thẳng song song, bạn có thể luyện tập thêm các bài tập sau:
Để giải bài tập về các góc và đường thẳng song song một cách hiệu quả, bạn nên:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 5 trang 115 SGK Toán 7 tập 2 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!