Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh, một trong những tiêu chí quan trọng để xác định hai tam giác có bằng nhau hay không. Chúng ta sẽ cùng nhau tìm hiểu điều kiện cần và đủ, cách áp dụng lý thuyết vào giải bài tập SGK Toán 7 - Cánh diều.
Giaitoan.edu.vn mang đến bài giảng chi tiết, dễ hiểu, kèm theo các ví dụ minh họa sinh động, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
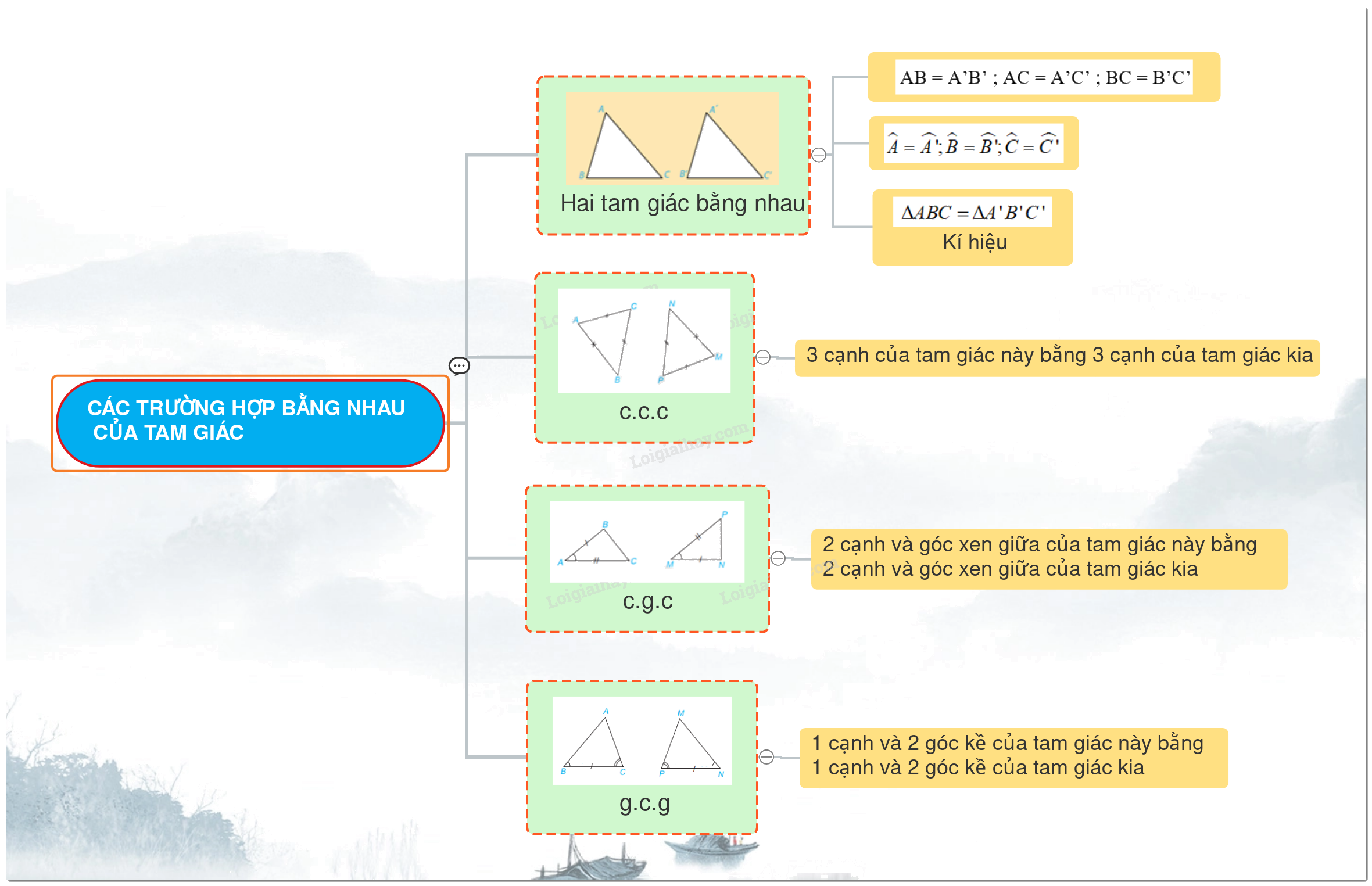
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
Xét 2 tam giác ABC và MNP có:
AB=MN
\(\widehat {BAC} = \widehat {NMP}\)
AC=MP
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
Trong chương trình Toán 7, việc nắm vững các trường hợp bằng nhau của tam giác là vô cùng quan trọng. Bài viết này sẽ đi sâu vào phân tích Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh (c-g-c), theo chương trình SGK Toán 7 - Cánh diều. Chúng ta sẽ cùng nhau khám phá định nghĩa, điều kiện áp dụng, và các ví dụ minh họa cụ thể.
Hai tam giác được gọi là bằng nhau nếu chúng có hai cạnh bằng nhau và góc xen giữa hai cạnh đó bằng nhau. Nói cách khác, nếu tam giác ABC và tam giác A'B'C' có:
Thì tam giác ABC bằng tam giác A'B'C' (ký hiệu: ΔABC = ΔA'B'C').
Việc chứng minh trường hợp bằng nhau này dựa trên việc sử dụng các tính chất của tam giác và các phép biến hình. Một cách chứng minh phổ biến là sử dụng phép chiếu vuông góc hoặc các tính chất của đường trung tuyến.
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, ∠A = ∠D. Chứng minh ΔABC = ΔDEF.
Giải:
Ví dụ 2: Cho hình vẽ (đính kèm hình vẽ minh họa tam giác ABC với AD là phân giác ∠BAC, D nằm trên BC). Biết AB = AC. Chứng minh ΔABD = ΔACD.
Giải:
Dưới đây là một số bài tập vận dụng để bạn luyện tập và củng cố kiến thức về Trường hợp bằng nhau thứ hai của tam giác:
Khi áp dụng Trường hợp bằng nhau thứ hai của tam giác, bạn cần đảm bảo rằng:
Ngoài Trường hợp bằng nhau thứ hai của tam giác (c-g-c), còn có các trường hợp bằng nhau khác như:
Việc nắm vững tất cả các trường hợp bằng nhau của tam giác sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế.