Bài học này cung cấp kiến thức nền tảng về phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ, một trong những chủ đề quan trọng của chương trình Toán 7 Cánh diều. Chúng ta sẽ cùng nhau khám phá định nghĩa, các tính chất và ứng dụng của phép tính này.
Nội dung được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Học sinh có thể sử dụng kiến thức này để giải các bài tập và ứng dụng vào thực tế.
I. Phép tính lũy thừa với số mũ tự nhiên
I. Phép tính lũy thừa với số mũ tự nhiên
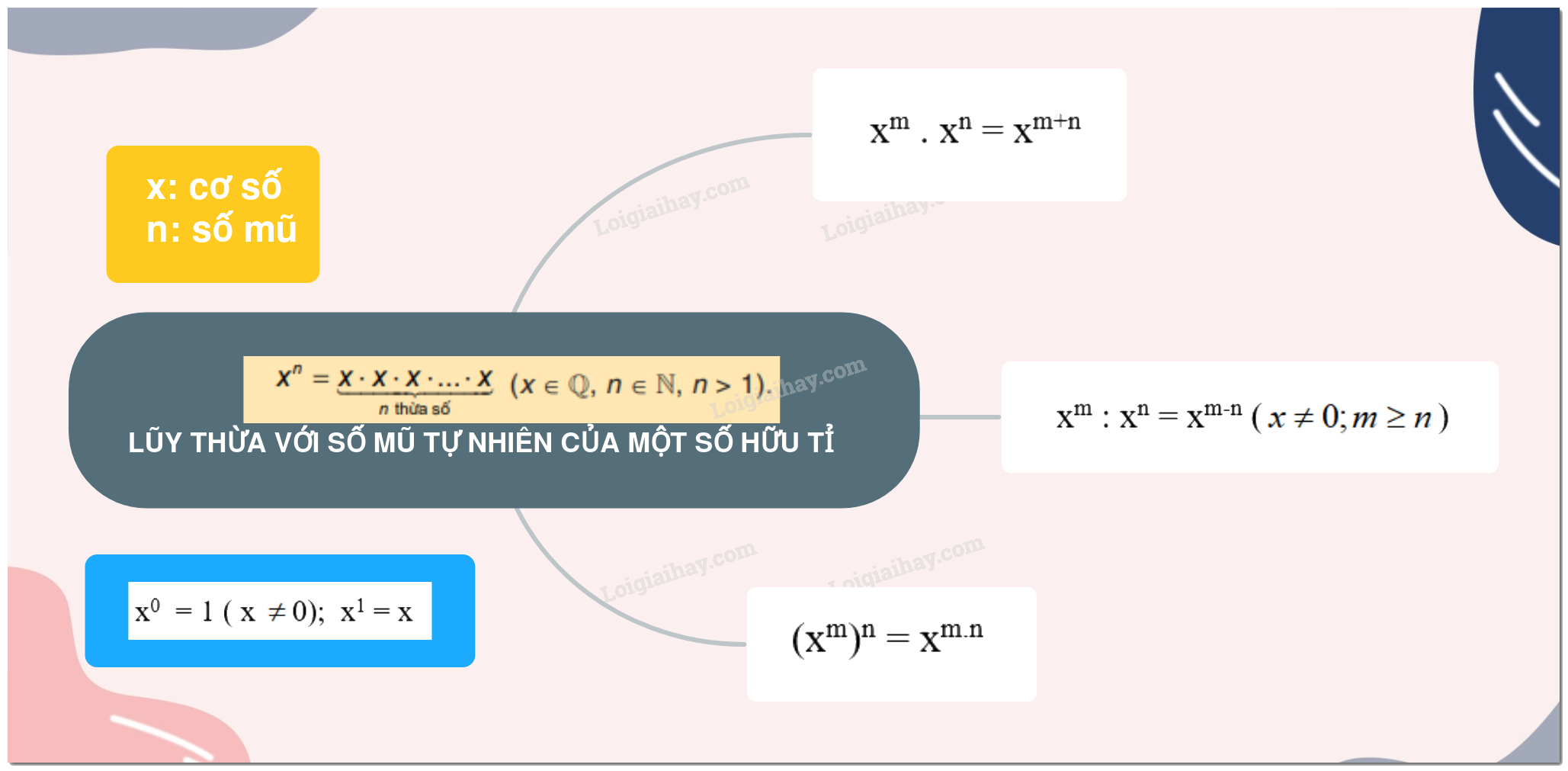
Lũy thừa bậc n của một số hữu tỉ x , kí hiệu xn , là tích của n thừa số x ( n là số tự nhiên lớn hợn 1)
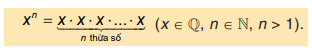
xn đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.
x: cơ số
n: số mũ
Quy ước: x0 = 1 ( x \( \ne \)0); x1 = x
Chú ý:
\(\begin{array}{l}{(x.y)^n} = {x^n}.{y^n}\\{(\frac{x}{y})^n} = \frac{{{x^n}}}{{{y^n}}}\end{array}\)
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ luôn dương
+ Lũy thừa số mũ lẻ của 1 số hữu tỉ âm luôn âm
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ dương luôn dương
II. Tích và thương hai lũy thừa cùng cơ số
+ Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ
xm . xn = xm+n
+ Khi chia 2 lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi lũy thừa của số chia
xm : xn = xm-n (\(x \ne 0;m \ge n\))
Ví dụ: 74 . 78 = 74+8 = 712
75 : (-7)2 = 75 : 72 = 75-2 = 73
III. Lũy thừa của lũy thừa
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.
(xm)n = xm.n
Ví dụ: [(-3)3]4 = (-3)3.4 = (-3)12
Phép tính lũy thừa là một trong những khái niệm cơ bản và quan trọng trong toán học, đặc biệt là ở chương trình Toán 7. Bài viết này sẽ trình bày chi tiết lý thuyết về phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ theo chương trình Cánh Diều, giúp học sinh nắm vững kiến thức và áp dụng vào giải bài tập.
Lũy thừa của một số hữu tỉ a với số mũ tự nhiên n (n > 0) là tích của n thừa số bằng a. Ký hiệu là an.
Ví dụ: 23 = 2 × 2 × 2 = 8
Trong đó:
Phép tính lũy thừa có một số tính chất quan trọng sau:
Ví dụ 1: Tính (3/4)2
(3/4)2 = (3/4) × (3/4) = 9/16
Ví dụ 2: Tính (23)2
(23)2 = 23 × 2 = 26 = 64
Ví dụ 3: Tính (1/2)0
(1/2)0 = 1
Hãy thực hiện các bài tập sau để củng cố kiến thức:
Khi thực hiện phép tính lũy thừa, cần chú ý đến các quy tắc về dấu:
Phép tính lũy thừa có nhiều ứng dụng trong thực tế, ví dụ như:
Hi vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ Toán 7 Cánh Diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập một cách hiệu quả.