Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 107 SGK Toán 7 tập 2 - Cánh diều. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải bài tập, nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp đáp án chính xác, dễ hiểu và các bài giảng chất lượng.
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh: a) GA = GD;
Đề bài
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:
a) GA = GD;
b) \(\Delta MBG = \Delta MCD\);
c) \(CD = 2GN\).
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất ba đường trung tuyến trong tam giác.
b) Chứng minh hai tam giác này bằng nhau theo trường hợp c.g.c.
c) Dựa vào kết quả phần b) để chứng minh \(CD = 2GN\).
Lời giải chi tiết
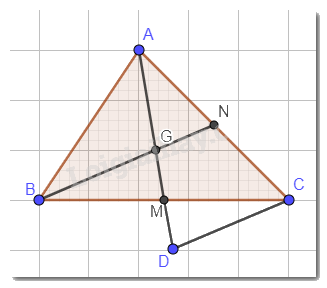
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD(= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = MD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).
Bài 3 trang 107 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về tam giác cân, tính chất đường trung tuyến trong tam giác, và các định lý liên quan đến góc trong tam giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết vấn đề.
Bài 3 yêu cầu học sinh chứng minh một số tính chất liên quan đến tam giác cân và đường trung tuyến. Cụ thể, bài tập thường xoay quanh việc chứng minh hai tam giác bằng nhau, từ đó suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau. Để giải quyết bài toán này, học sinh cần:
Để giúp các em hiểu rõ hơn về cách giải bài 3 trang 107 SGK Toán 7 tập 2 - Cánh diều, chúng ta sẽ đi vào phân tích từng bước giải cụ thể:
Đọc kỹ đề bài, xác định các giả thiết và kết luận cần chứng minh. Vẽ hình minh họa để dễ dàng hình dung bài toán.
Dựa trên các giả thiết và kiến thức đã học, lập luận logic để chứng minh kết luận. Sử dụng các định lý, tính chất và trường hợp bằng nhau của tam giác một cách hợp lý.
Sau khi chứng minh xong, kiểm tra lại các bước lập luận và kết quả để đảm bảo tính chính xác.
Đề bài: Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC. Chứng minh AM vuông góc với BC.
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập về tam giác cân và đường trung tuyến, các em có thể tự giải thêm các bài tập tương tự trong SGK và sách bài tập Toán 7 tập 2. Ngoài ra, các em cũng có thể tham khảo các bài giảng online và tài liệu học tập khác để nâng cao trình độ.
Bài 3 trang 107 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng chứng minh hình học và vận dụng các kiến thức về tam giác cân. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết bài toán này và đạt kết quả tốt trong môn Toán.