Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 106 và 107 sách giáo khoa Toán 7 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Cho định lí: “ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”. a) Vẽ hình minh họa nội dung định lí trên. b) Viết giả thiết và kết luận của định lí trên. c) Chứng tỏ định lí trên là đúng.
Chứng minh định lí: “ Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau”.
Phương pháp giải:
- Phần nằm giữa từ “ Nếu” và từ “ thì” là giả thiết
- Phần nằm sau từ “ thì” là kết luận
Để chứng minh định lí, ta cần xuất phát từ giả thiết, định nghĩa, tính chất liên quan.
Lời giải chi tiết:
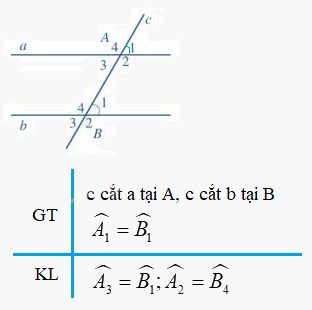
Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}\) (gt)
\(\widehat {{A_3}} = \widehat {{A_1}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{A_3}} = \widehat {{B_1}}\) ( cùng bằng \(\widehat {{A_1}}\))
Mà \(\widehat {{A_2}} + \widehat {{A_3}} = 180^\circ ;\widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \) ( 2 góc kề bù)
\( \Rightarrow \widehat {{A_2}} = \widehat {{B_4}}\)
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
Phương pháp giải:
Vẽ hình
Giả thiết là điều đề bài cho
Kết luận là điều cần chứng minh
Để chứng minh định lí, ta cần xuất phát từ giả thiết, định nghĩa, tính chất liên quan
Lời giải chi tiết:
a)
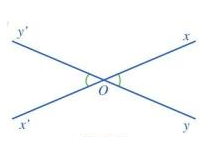
b)
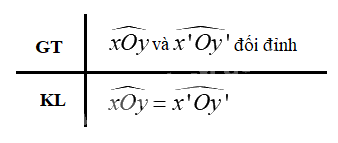
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
Phương pháp giải:
Vẽ hình
Giả thiết là điều đề bài cho
Kết luận là điều cần chứng minh
Để chứng minh định lí, ta cần xuất phát từ giả thiết, định nghĩa, tính chất liên quan
Lời giải chi tiết:
a)
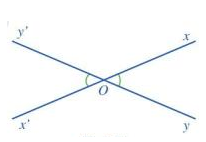
b)
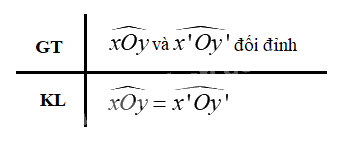
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Chứng minh định lí: “ Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau”.
Phương pháp giải:
- Phần nằm giữa từ “ Nếu” và từ “ thì” là giả thiết
- Phần nằm sau từ “ thì” là kết luận
Để chứng minh định lí, ta cần xuất phát từ giả thiết, định nghĩa, tính chất liên quan.
Lời giải chi tiết:
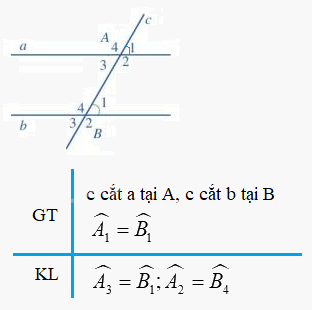
Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}\) (gt)
\(\widehat {{A_3}} = \widehat {{A_1}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{A_3}} = \widehat {{B_1}}\) ( cùng bằng \(\widehat {{A_1}}\))
Mà \(\widehat {{A_2}} + \widehat {{A_3}} = 180^\circ ;\widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \) ( 2 góc kề bù)
\( \Rightarrow \widehat {{A_2}} = \widehat {{B_4}}\)
Mục II trong SGK Toán 7 tập 1 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Mục II bao gồm các bài tập đa dạng, từ việc thực hiện các phép tính đơn giản đến việc giải các bài toán có tính ứng dụng cao. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ và các tính chất của các phép toán.
Bài tập này yêu cầu học sinh tìm giá trị của x trong các phương trình chứa số hữu tỉ. Để giải bài tập này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng đơn giản và tìm ra giá trị của x.
Bài tập này yêu cầu học sinh vận dụng kiến thức về số hữu tỉ để giải các bài toán thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các dữ kiện quan trọng và xây dựng phương trình phù hợp.
Ví dụ: Một người nông dân có một mảnh đất hình chữ nhật với chiều dài là 10m và chiều rộng là 5m. Người nông dân muốn chia mảnh đất thành các ô vuông nhỏ bằng nhau. Hỏi người nông dân có thể chia mảnh đất thành bao nhiêu ô vuông nhỏ?
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về số hữu tỉ:
Hy vọng rằng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục II trang 106, 107 SGK Toán 7 tập 1 - Cánh diều. Chúc các em học tập tốt!