Chào mừng các em học sinh đến với bài học về Lý thuyết Tập hợp R các số thực trong chương trình Toán 7 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng về tập hợp số thực, bao gồm số hữu tỉ và số vô tỉ.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất và các phép toán trên tập hợp số thực, đồng thời luyện tập thông qua các bài tập minh họa.
I. Tập hợp số thực
I. Tập hợp số thực
1. Số thực
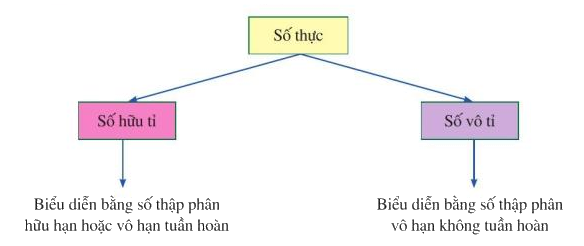
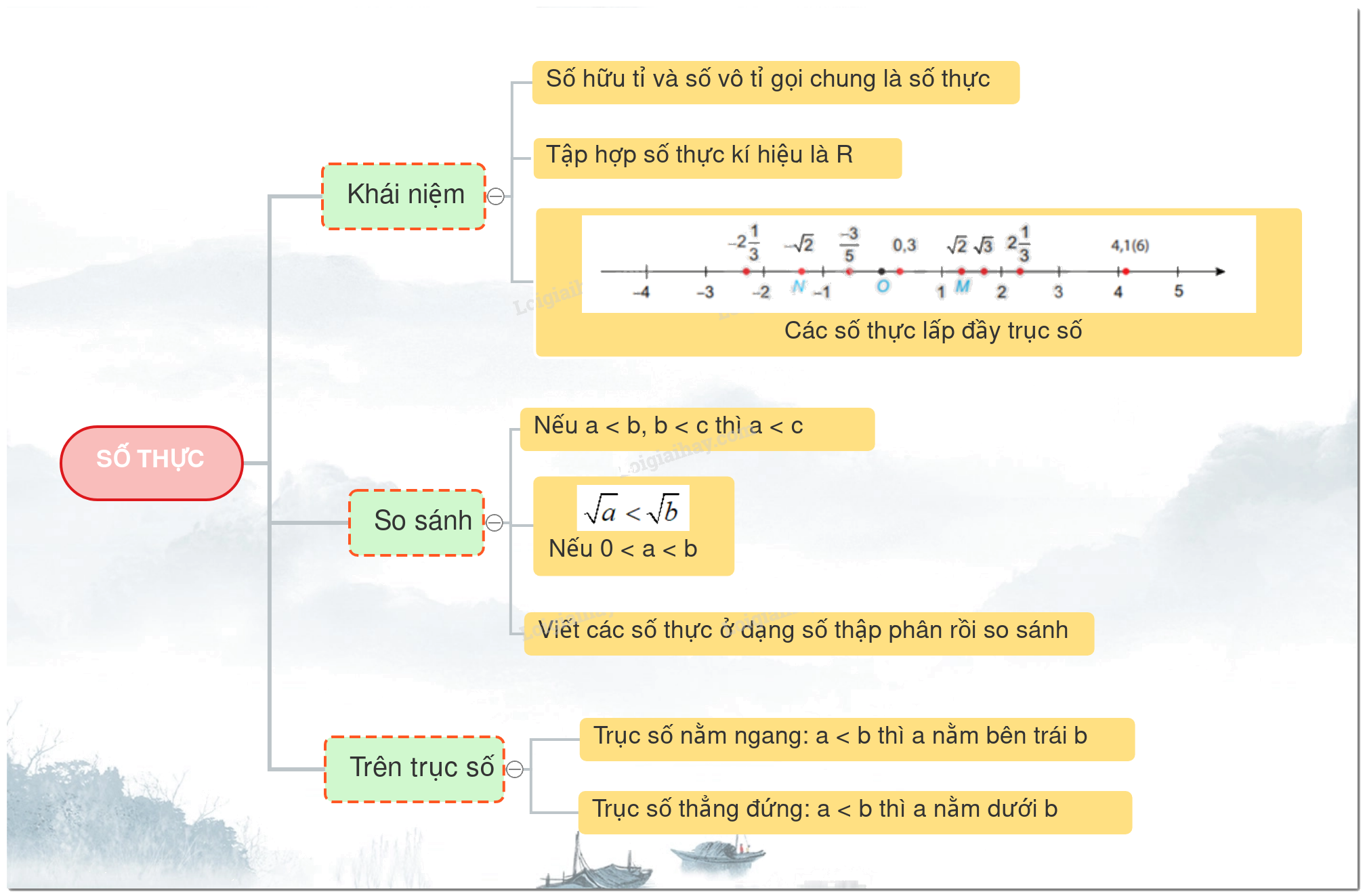
* Số hữu tỉ và số vô tỉ gọi chung là số thực
* Tập hợp các số thực được kí hiệu là R.
2. Biểu diễn thập phân của số thực
II. Biểu diễn số thực trên trục số
+ Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
* Trục số thực được biểu diễn bởi 1 số điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Chú ý: Các số thực lấp đầy trục số.
III. Số đối của một số thực
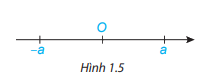
+ Mỗi số thực a đều có một số đối là –a
+ Trên trục số, 2 điểm biểu diễn 2 số thực đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
+ Số đối của số 0 là 0
Ví dụ: -\(\sqrt 5 \) là số đối của \(\sqrt 5 \)
IV. So sánh hai số thực
1. So sánh 2 số thực
+ Với 2 số thực a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
+ Cho 3 số thực a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)
+ Các số thực lớn hơn 0 gọi là các số thực dương.
+ Các số thực nhỏ hơn 0 gọi là các số thực âm.
+ Số 0 không là số thực âm, cũng không là số thực dương.
2. Cách so sánh hai số thực:
Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.
* Các số thực đều viết được dưới dạng số thập phân ( hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.
Ví dụ:
0,322 … < 0,324… nên 0,3(2) < 0,324…
Chú ý: Nếu 0 < a < b thì \(\sqrt a < \sqrt b \)
Ví dụ: Vì 3 < 4 nên \(\sqrt 3 < \sqrt 4 = 2\)
3. Minh họa trên trục số
* Trên trục số nằm ngang:
+ Nếu a < b thì điểm a nằm bên trái điểm b
+ Nếu điểm a nằm bên trái điểm b thì a < b
+ Các điểm nằm bên trái gốc O biểu diễn số hữu tỉ âm; các điểm nằm bên phải gốc O biểu diễn số hữu tỉ dương.
* Trên trục số thẳng đứng:
+ Nếu a < b thì điểm a nằm phía dưới điểm b
+ Nếu điểm a nằm phía dưới điểm b thì a < b
+ Các điểm nằm phía dưới gốc O biểu diễn số hữu tỉ âm; các điểm nằm phía trên gốc O biểu diễn số hữu tỉ dương.
Tập hợp số thực (ký hiệu là R) là một trong những tập hợp số quan trọng nhất trong toán học. Nó bao gồm tất cả các số hữu tỉ (Q) và số vô tỉ (I). Để hiểu rõ hơn về tập hợp này, chúng ta cần nắm vững các khái niệm cơ bản sau:
Số hữu tỉ là số có thể biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0. Ví dụ: 1/2, -3/4, 5, 0.5 (tương đương 1/2).
Số vô tỉ là số không thể biểu diễn dưới dạng phân số a/b. Chúng có phần thập phân vô hạn không tuần hoàn. Ví dụ: √2, π, e.
Tập hợp số thực (R) bao gồm tất cả các số hữu tỉ (Q) và số vô tỉ (I). R = Q ∪ I. Tập hợp số thực được biểu diễn trên trục số, bao gồm tất cả các điểm trên trục số.
Các phép toán cộng, trừ, nhân, chia đều được định nghĩa trên tập hợp số thực. Tuy nhiên, cần lưu ý một số trường hợp:
Tập hợp số thực có các tính chất quan trọng sau:
Mỗi số thực đều có thể được biểu diễn bằng một điểm duy nhất trên trục số. Số thực lớn hơn 0 nằm bên phải gốc tọa độ (0), số thực nhỏ hơn 0 nằm bên trái gốc tọa độ.
Có thể so sánh hai số thực bằng cách sử dụng các dấu >, <, =. Số thực nào nằm bên phải trên trục số thì lớn hơn.
Ví dụ 1: So sánh hai số thực 3.14 và π. Ta biết π ≈ 3.14159, do đó 3.14 < π.
Ví dụ 2: Thực hiện phép tính (1/2) + √2. Kết quả là một số vô tỉ, thuộc tập hợp số thực.
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Tập hợp R các số thực Toán 7 Cánh diều. Chúc các em học tập tốt!