Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 57, 58, 59 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Thực hiện phép trừ trong mỗi trường hợp sau: b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
a) Thực hiện phép trừ trong mỗi trường hợp sau: \(2{x^2} - 6{x^2}\); \(a{x^k} - b{x^k}\)(k \(\in\) N*).
b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
Phương pháp giải:
a) Để thực hiện phép trừ trong các phép tính, ta giữ nguyên biến và trừ các hệ số cùng biến cho nhau.
b) Rút ra quy tắc trừ hai đơn thức có cùng số mũ của biến từ cách thực hiện phần a.
Lời giải chi tiết:
a) \(2{x^2} - 6{x^2} = (2 - 6){x^2} = - 4{x^2}\);
\(a{x^k} - b{x^k} = (a - b){x^k}\).
b) Muốn trừ hai đơn thức có cùng số mũ của biến, ta giữ nguyên biến và tính hiệu của các hệ số có trong đơn thức.
Cho hai đa thức:
\(P(x) = - 3{x^2} + 2 + 7x\) và \(Q(x) = - 4x + 5{x^2} + 1\).
a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.
b) Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc.
c) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính hiệu P(x) – Q(x) bằng cách thực hiện phép tính trong từng nhóm.
Phương pháp giải:
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. (Ở cả 2 đa thức đã cho thì số mũ lớn nhất là 2 rồi đến 1 và 0).
b) Viết hiệu hai đa thức theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Thực hiện phép tính sau khi đã nhóm.
Lời giải chi tiết:
a) \(P(x) = - 3{x^2} + 2 + 7x = - 3{x^2} + 7x + 2\);
\(Q(x) = - 4x + 5{x^2} + 1 = 5{x^2} - 4x + 1\).
b) \(P(x) - Q(x) = - 3{x^2} + 7x + 2 - (5{x^2} - 4x + 1)\).
c) \(\begin{array}{l}P(x) - Q(x) = - 3{x^2} + 7x + 2 - (5{x^2} - 4x + 1)\\ = - 3{x^2} + 7x + 2 - 5{x^2} + 4x - 1\\ = ( - 3{x^2} - 5{x^2}) + (7x + 4x) + (2 - 1)\end{array}\)
d) \(\begin{array}{l}P(x) - Q(x) = ( - 3{x^2} - 5{x^2}) + (7x + 4x) + (2 - 1)\\ = - 8{x^2} + 11x + 1\end{array}\)
Cho hai đa thức:
\(P(x) = 2{x^2} - 5x - \dfrac{1}{3}\)
và \(Q(x) = - 6{x^4} + 5{x^2} + \dfrac{2}{3} + 3x\).
Tính hiệu P(x) – Q(x).
Phương pháp giải:
Xem lại cách thức trừ hai đa thức theo cột dọc:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Lời giải chi tiết:
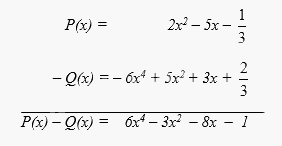
Tính hiệu P(x) – Q(x) bằng hai cách, trong đó:
\(\begin{array}{l}P(x) = 6{x^3} + 8{x^2} + 5x - 2;\\Q(x) = - 9{x^3} + 6{x^2} + 3 + 2x.\end{array}\)
Phương pháp giải:
Nhớ lại cách thức trừ hai đa thức theo cột dọc và theo hàng ngang:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Lời giải chi tiết:
Theo cột dọc:
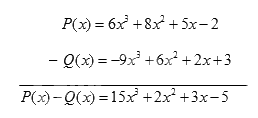
Theo hàng ngang:
\(\begin{array}{l}P(x) - Q(x) = 6{x^3} + 8{x^2} + 5x - 2 - ( - 9{x^3} + 6{x^2} + 2x + 3)\\ = 6{x^3} + 8{x^2} + 5x - 2 + 9{x^3} - 6{x^2} - 2x - 3\\ = (6 + 9){x^3} + (8 - 6){x^2} + (5 - 2)x + ( - 2 - 3)\\ = 15{x^3} + 2{x^2} + 3x - 5\end{array}\)
Cho hai đa thức:
\(P(x) = 4{x^2} + 1 + 3x\) và \(Q(x) = 5x + 2{x^2} + 3\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
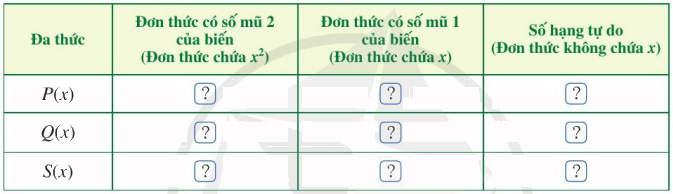
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức S(x).
Phương pháp giải:
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức S(x) dựa vào kết quả phần b).
Lời giải chi tiết:
a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\);
\(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)
II. Trừ hai đa thức một biến
a) Thực hiện phép trừ trong mỗi trường hợp sau: \(2{x^2} - 6{x^2}\); \(a{x^k} - b{x^k}\)(k \(\in\) N*).
b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
Phương pháp giải:
a) Để thực hiện phép trừ trong các phép tính, ta giữ nguyên biến và trừ các hệ số cùng biến cho nhau.
b) Rút ra quy tắc trừ hai đơn thức có cùng số mũ của biến từ cách thực hiện phần a.
Lời giải chi tiết:
a) \(2{x^2} - 6{x^2} = (2 - 6){x^2} = - 4{x^2}\);
\(a{x^k} - b{x^k} = (a - b){x^k}\).
b) Muốn trừ hai đơn thức có cùng số mũ của biến, ta giữ nguyên biến và tính hiệu của các hệ số có trong đơn thức.
Cho hai đa thức:
\(P(x) = 4{x^2} + 1 + 3x\) và \(Q(x) = 5x + 2{x^2} + 3\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
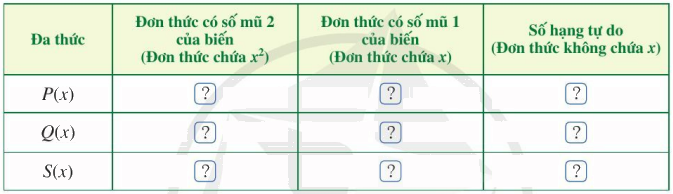
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức S(x).
Phương pháp giải:
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức S(x) dựa vào kết quả phần b).
Lời giải chi tiết:
a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\);
\(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)
Cho hai đa thức:
\(P(x) = 2{x^2} - 5x - \dfrac{1}{3}\)
và \(Q(x) = - 6{x^4} + 5{x^2} + \dfrac{2}{3} + 3x\).
Tính hiệu P(x) – Q(x).
Phương pháp giải:
Xem lại cách thức trừ hai đa thức theo cột dọc:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Lời giải chi tiết:
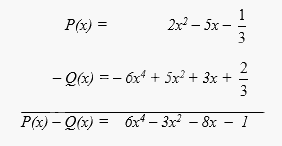
Cho hai đa thức:
\(P(x) = - 3{x^2} + 2 + 7x\) và \(Q(x) = - 4x + 5{x^2} + 1\).
a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.
b) Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc.
c) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính hiệu P(x) – Q(x) bằng cách thực hiện phép tính trong từng nhóm.
Phương pháp giải:
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. (Ở cả 2 đa thức đã cho thì số mũ lớn nhất là 2 rồi đến 1 và 0).
b) Viết hiệu hai đa thức theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Thực hiện phép tính sau khi đã nhóm.
Lời giải chi tiết:
a) \(P(x) = - 3{x^2} + 2 + 7x = - 3{x^2} + 7x + 2\);
\(Q(x) = - 4x + 5{x^2} + 1 = 5{x^2} - 4x + 1\).
b) \(P(x) - Q(x) = - 3{x^2} + 7x + 2 - (5{x^2} - 4x + 1)\).
c) \(\begin{array}{l}P(x) - Q(x) = - 3{x^2} + 7x + 2 - (5{x^2} - 4x + 1)\\ = - 3{x^2} + 7x + 2 - 5{x^2} + 4x - 1\\ = ( - 3{x^2} - 5{x^2}) + (7x + 4x) + (2 - 1)\end{array}\)
d) \(\begin{array}{l}P(x) - Q(x) = ( - 3{x^2} - 5{x^2}) + (7x + 4x) + (2 - 1)\\ = - 8{x^2} + 11x + 1\end{array}\)
Tính hiệu P(x) – Q(x) bằng hai cách, trong đó:
\(\begin{array}{l}P(x) = 6{x^3} + 8{x^2} + 5x - 2;\\Q(x) = - 9{x^3} + 6{x^2} + 3 + 2x.\end{array}\)
Phương pháp giải:
Nhớ lại cách thức trừ hai đa thức theo cột dọc và theo hàng ngang:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Lời giải chi tiết:
Theo cột dọc:
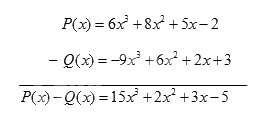
Theo hàng ngang:
\(\begin{array}{l}P(x) - Q(x) = 6{x^3} + 8{x^2} + 5x - 2 - ( - 9{x^3} + 6{x^2} + 2x + 3)\\ = 6{x^3} + 8{x^2} + 5x - 2 + 9{x^3} - 6{x^2} - 2x - 3\\ = (6 + 9){x^3} + (8 - 6){x^2} + (5 - 2)x + ( - 2 - 3)\\ = 15{x^3} + 2{x^2} + 3x - 5\end{array}\)
Mục II trong SGK Toán 7 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như các phép biến đổi đơn giản với đa thức, hoặc các bài toán liên quan đến biểu thức đại số. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán trong mục này là rất quan trọng để chuẩn bị cho các kiến thức nâng cao hơn trong chương trình học.
Bài tập này thường yêu cầu học sinh thực hiện các phép toán đơn giản với đa thức, ví dụ như cộng, trừ, nhân đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với đa thức, bao gồm quy tắc dấu ngoặc, quy tắc nhân đơn thức với đa thức, và quy tắc nhân đa thức với đa thức.
Ví dụ:
Cho hai đa thức A = 2x2 + 3x - 1 và B = -x2 + x + 2. Tính A + B và A - B.
Lời giải:
Bài tập này có thể yêu cầu học sinh phân tích đa thức thành nhân tử. Việc phân tích đa thức thành nhân tử giúp đơn giản hóa biểu thức và giải quyết các bài toán phức tạp hơn. Các phương pháp phân tích đa thức thành nhân tử thường được sử dụng bao gồm đặt nhân tử chung, sử dụng hằng đẳng thức, và nhóm các số hạng.
Ví dụ:
Phân tích đa thức x2 - 4 thành nhân tử.
Lời giải:
x2 - 4 = (x - 2)(x + 2) (Sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b))
Bài tập này có thể là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức đã học để giải quyết một vấn đề cụ thể. Để giải bài toán này, học sinh cần đọc kỹ đề bài, xác định các yếu tố quan trọng, và xây dựng phương trình hoặc biểu thức toán học phù hợp.
Ví dụ:
Một khu vườn hình chữ nhật có chiều dài là 2x + 3 và chiều rộng là x - 1. Tính diện tích của khu vườn.
Lời giải:
Diện tích của khu vườn là (2x + 3)(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và các mẹo giải toán hiệu quả được cung cấp trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục II trang 57, 58, 59 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt!