Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 112 và 113 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
I. Đường trung trực của tam giác
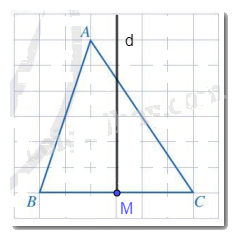
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.
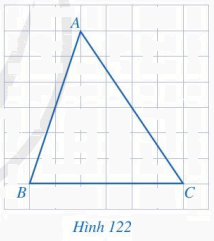
Phương pháp giải:
Đường trung trực là đường thẳng đi qua trung điểm của cạnh và vuông góc cạnh tại trung điểm đó.
Lời giải chi tiết:
Lấy M là trung điểm của đoạn thẳng BC. Đường thẳng d là đường thẳng đi qua M và vuông góc với BC.
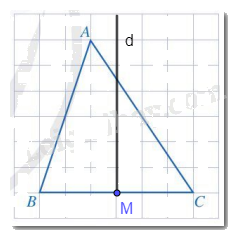
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Phương pháp giải:
Chứng minh AD là đường trung trực của tam giác ABC ta chứng minh D là trung điểm của BC và \(AD \bot BC\)
Lời giải chi tiết:
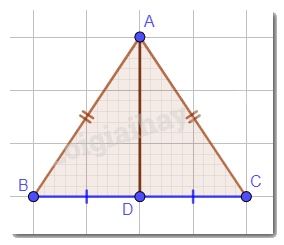
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\)D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.
I. Đường trung trực của tam giác
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.
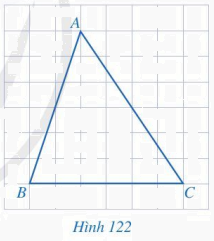
Phương pháp giải:
Đường trung trực là đường thẳng đi qua trung điểm của cạnh và vuông góc cạnh tại trung điểm đó.
Lời giải chi tiết:
Lấy M là trung điểm của đoạn thẳng BC. Đường thẳng d là đường thẳng đi qua M và vuông góc với BC.
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Phương pháp giải:
Chứng minh AD là đường trung trực của tam giác ABC ta chứng minh D là trung điểm của BC và \(AD \bot BC\)
Lời giải chi tiết:
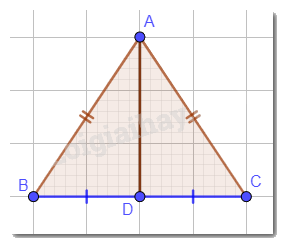
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\)D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.
Mục I trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải toán. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Chúng ta sẽ cùng nhau đi qua từng bài tập trong mục I trang 112 và 113, phân tích đề bài, tìm ra phương pháp giải phù hợp và trình bày lời giải một cách rõ ràng, dễ hiểu.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, ta cần xác định các đơn thức đồng dạng và cộng (hoặc trừ) các hệ số của chúng.
Ví dụ: Thu gọn đa thức 3x2 + 5x - 2x2 + x - 4.
Lời giải: 3x2 + 5x - 2x2 + x - 4 = (3x2 - 2x2) + (5x + x) - 4 = x2 + 6x - 4.
Bài tập này yêu cầu học sinh tìm bậc của đa thức đã cho. Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó.
Ví dụ: Tìm bậc của đa thức 2x3 - 5x2 + x - 1.
Lời giải: Bậc của đa thức 2x3 - 5x2 + x - 1 là 3.
Bài tập này yêu cầu học sinh tính giá trị của đa thức tại một giá trị cụ thể của biến. Để tính giá trị của đa thức, ta thay giá trị của biến vào đa thức và thực hiện các phép tính.
Ví dụ: Tính giá trị của đa thức x2 + 2x - 1 tại x = 2.
Lời giải: Thay x = 2 vào đa thức x2 + 2x - 1, ta được: 22 + 2(2) - 1 = 4 + 4 - 1 = 7.
Các bài tập ứng dụng yêu cầu học sinh sử dụng kiến thức về đa thức để giải các bài toán thực tế. Ví dụ, bài toán về tính diện tích, chu vi của hình chữ nhật khi chiều dài và chiều rộng được biểu diễn bằng các biểu thức đại số.
Khi giải các bài tập về đa thức, cần chú ý đến các quy tắc về dấu, thứ tự thực hiện các phép toán, và các hằng đẳng thức đại số. Việc nắm vững các quy tắc này sẽ giúp bạn giải toán nhanh chóng và chính xác hơn.
Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục I trang 112, 113 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Thu gọn đa thức |
| Bài 2 | Tìm bậc của đa thức |
| Bài 3 | Tính giá trị của đa thức |
| Bài 4 | Ứng dụng của đa thức |