Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục II trang 98 SGK Toán 7 tập 2 - Cánh diều. Bài viết này được giaitoan.edu.vn biên soạn nhằm giúp các em hiểu rõ hơn về kiến thức và phương pháp giải các bài toán trong chương trình học.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, kèm theo các bước giải chi tiết và giải thích rõ ràng, giúp các em tự tin hơn trong quá trình học tập.
II. Quan hệ giữa đường vuông góc và đường xiên
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A lên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Phương pháp giải:
Trong một tam giác, đường vuông góc luôn nhỏ hơn đường xiên.
Trong một tam giác, cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.
Lời giải chi tiết:
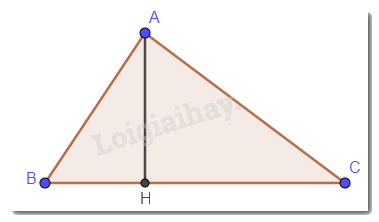
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.
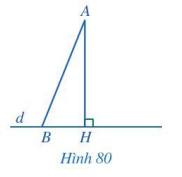
Giả sử AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d (Hình 80). Trong tam giác AHB, hãy so sánh:
a) Số đo góc AHB và số đo góc ABH;
b) Độ dài cạnh AB và độ dài cạnh AH.
Phương pháp giải:
a) Tổng ba góc trong một tam giác bằng 180°.
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.
Lời giải chi tiết:
a) Tổng ba góc trong một tam giác bằng 180°. Mà góc H bằng 90° nên tổng hai góc còn lại trong tam giác bằng \(180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {AHB} > \widehat {ABH}\).
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn. Vậy AB > AH (AB đối diện với góc H; AH đối diện với góc B).
II. Quan hệ giữa đường vuông góc và đường xiên
Giả sử AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d (Hình 80). Trong tam giác AHB, hãy so sánh:
a) Số đo góc AHB và số đo góc ABH;
b) Độ dài cạnh AB và độ dài cạnh AH.
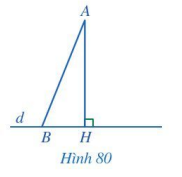
Phương pháp giải:
a) Tổng ba góc trong một tam giác bằng 180°.
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.
Lời giải chi tiết:
a) Tổng ba góc trong một tam giác bằng 180°. Mà góc H bằng 90° nên tổng hai góc còn lại trong tam giác bằng \(180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {AHB} > \widehat {ABH}\).
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn. Vậy AB > AH (AB đối diện với góc H; AH đối diện với góc B).
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A lên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Phương pháp giải:
Trong một tam giác, đường vuông góc luôn nhỏ hơn đường xiên.
Trong một tam giác, cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.
Lời giải chi tiết:
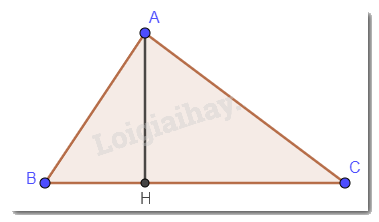
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.
Mục II trang 98 SGK Toán 7 tập 2 - Cánh diều tập trung vào việc vận dụng các kiến thức đã học về tam giác cân, tam giác đều để giải các bài toán thực tế. Các bài tập thường yêu cầu học sinh chứng minh tính chất, tính góc, hoặc tìm độ dài cạnh của tam giác. Để giải tốt các bài tập này, học sinh cần nắm vững định nghĩa, tính chất của tam giác cân, tam giác đều, cũng như các định lý liên quan đến góc và cạnh trong tam giác.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số khái niệm quan trọng:
Các bài tập trong mục II trang 98 SGK Toán 7 tập 2 - Cánh diều thường thuộc các dạng sau:
Bài 1: (Đề bài cụ thể của bài 1)...
Lời giải:
...
Bài 2: (Đề bài cụ thể của bài 2)...
Lời giải:
...
Để giải bài tập mục II trang 98 SGK Toán 7 tập 2 - Cánh diều một cách hiệu quả, các em cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể thử sức với các bài tập vận dụng nâng cao sau:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải các bài tập mục II trang 98 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!