Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 92, 93 sách giáo khoa Toán 7 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Tìm tổng số đo của góc...Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau. a) Hai góc xOt và yOt có kề nhau không?
Tìm tổng số đo của góc 110 \(^\circ \) và 70 \(^\circ \)
Phương pháp giải:
Tìm tổng số đo của góc
Lời giải chi tiết:
2 góc có tổng số đo là: 110 \(^\circ \)+70 \(^\circ \) = 180 \(^\circ \)
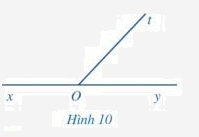
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
Phương pháp giải:
a) 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
b) Dựa vào tính chất 2 góc kề nhau, tính tổng số đo
Lời giải chi tiết:
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng
Tính góc xOt trong Hình 12

Phương pháp giải:
Sử dụng tính chất : Tổng số đo của 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
Ta có: \(\widehat {xOt} + \widehat {tOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {xOt} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
Tìm tổng số đo của góc 110 \(^\circ \) và 70 \(^\circ \)
Phương pháp giải:
Tìm tổng số đo của góc
Lời giải chi tiết:
2 góc có tổng số đo là: 110 \(^\circ \)+70 \(^\circ \) = 180 \(^\circ \)
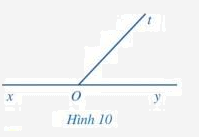
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
Phương pháp giải:
a) 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
b) Dựa vào tính chất 2 góc kề nhau, tính tổng số đo
Lời giải chi tiết:
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng
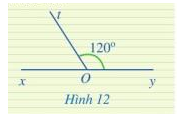
Tính góc xOt trong Hình 12
Phương pháp giải:
Sử dụng tính chất : Tổng số đo của 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
Ta có: \(\widehat {xOt} + \widehat {tOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {xOt} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
Mục II trong SGK Toán 7 tập 1 - Cánh diều tập trung vào các bài tập về số hữu tỉ, các phép toán trên số hữu tỉ và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng quan trọng cho việc học tập các kiến thức toán học ở các lớp trên.
Bài tập 1 yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ và các phép toán trên số hữu tỉ.
Ví dụ:
Bài tập 2 yêu cầu học sinh tìm số hữu tỉ thích hợp để điền vào chỗ trống. Để giải bài tập này, học sinh cần sử dụng các kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ để tìm ra số hữu tỉ thỏa mãn điều kiện của bài toán.
Ví dụ:
a) ... + 2/5 = 1. Đáp án: 3/5
b) ... - 1/3 = 1/2. Đáp án: 5/6
Bài tập 3 thường liên quan đến các bài toán ứng dụng số hữu tỉ vào thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các thông tin quan trọng và sử dụng các kiến thức về số hữu tỉ để giải quyết bài toán.
Ví dụ: Một cửa hàng bán một chiếc áo với giá gốc là 200.000 đồng. Cửa hàng giảm giá 10% cho chiếc áo đó. Hỏi giá bán chiếc áo sau khi giảm giá là bao nhiêu?
Lời giải:
Số tiền giảm giá là: 200.000 * 10% = 20.000 đồng
Giá bán chiếc áo sau khi giảm giá là: 200.000 - 20.000 = 180.000 đồng
Bài tập 4 có thể là một bài toán tổng hợp, yêu cầu học sinh vận dụng nhiều kiến thức và kỹ năng về số hữu tỉ để giải quyết. Để giải bài tập này, học sinh cần phân tích đề bài, xác định các bước giải và thực hiện các phép toán một cách chính xác.
Để học tốt môn Toán 7, các em cần thường xuyên luyện tập, làm bài tập và tìm hiểu các kiến thức mới. Ngoài ra, các em có thể tham gia các khóa học toán online hoặc tìm kiếm sự giúp đỡ của các thầy cô giáo, bạn bè.
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!