Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 67 SGK Toán 7 tập 2 - Cánh diều. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Tính
Đề bài
Tính:
a) \(({x^2} - 2x + 1):(x - 1)\);
b) \(({x^3} + 2{x^2} + x):({x^2} + x)\);
c) \(( - 16{x^4} + 1):( - 4{x^2} + 1)\);
d) \(( - 32{x^5} + 1):( - 2x + 1)\).
Phương pháp giải - Xem chi tiết
Để chia một đa thức cho một đa thức khác không (hai đa thức đều đã thu gọn và sắp xếp theo số mũ giảm dần), ta làm như sau:
Bước 1:
- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
- Nhân kết quả trên với đa thức chia và đặt dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
Lời giải chi tiết
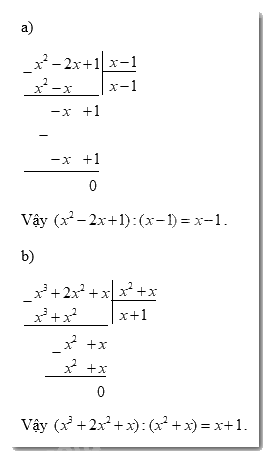
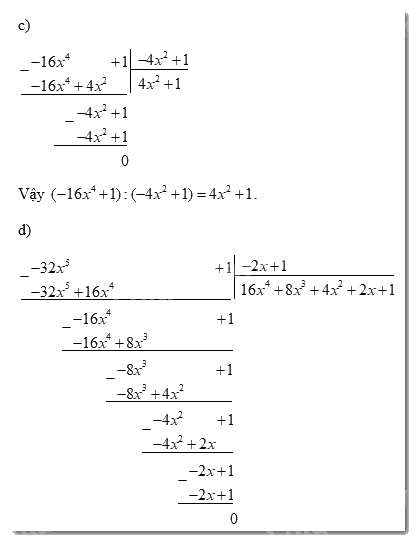
Vậy \(( - 32{x^5} + 1):( - 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).
Bài 3 trang 67 SGK Toán 7 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán liên quan đến tính chất của góc.
Bài 3: Quan sát Hình 7, biết a // b và ∠A1 = 40°. Tính số đo của các góc còn lại trên hình.
Lời giải:
Giả sử ta có hai đường thẳng song song c và d bị cắt bởi đường thẳng e. Biết ∠C1 = 60°. Hãy tính ∠D1 (∠D1 là góc so le trong với ∠C1).
Lời giải: Vì c // d và ∠C1 và ∠D1 là hai góc so le trong, nên ∠D1 = ∠C1 = 60°.
1. Cho hai đường thẳng m và n song song, bị cắt bởi đường thẳng p. Biết ∠M1 = 70°. Tính ∠N1 (∠N1 là góc đồng vị với ∠M1).
2. Cho hai đường thẳng r và s song song, bị cắt bởi đường thẳng q. Biết ∠R1 = 110°. Tính ∠S2 (∠S2 là góc trong cùng phía với ∠R1).
Việc nắm vững lý thuyết và phương pháp giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song là rất quan trọng trong chương trình Toán 7. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài 3 trang 67 SGK Toán 7 tập 2 - Cánh diều và tự tin giải quyết các bài tập tương tự.