Chào mừng bạn đến với bài học về Lý thuyết Làm tròn và Ước lượng trong chương trình Toán 7 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về cách làm tròn số và ước lượng kết quả trong các bài toán thực tế.
Chúng ta sẽ cùng nhau tìm hiểu các khái niệm, quy tắc và ví dụ minh họa để bạn có thể áp dụng một cách hiệu quả trong quá trình học tập và giải bài tập.
I. Làm tròn số
I. Làm tròn số
1. Số làm tròn
Ở nhiều tình huống, ta cần tìm 1 số thực xấp xỉ với số thực đã cho để tiện ghi nhớ, đo đạc, tính toán. Số thực tìm được như thế gọi là số làm tròn.
2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước
Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.
Khi làm tròn đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.
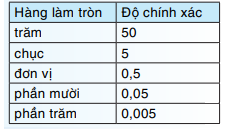
Ví dụ: Làm tròn số 2,13452….với độ chính xác 0,005, tức là làm tròn số 2,13452…. đến hàng phần trăm, ta được 2,13.
Chú ý: Trong đo đạc và tính toán, ta cố gắng làm tròn với độ chính xác càng nhỏ càng tốt.
II. Ước lượng
Đôi khi ta không quá quan tâm đến kết quả chính xác mà chỉ cần ước lượng kết quả, nghĩa là tìm một số gần sát với kết quả chính xác.
Ví dụ:
Ước lượng kết quả của phép tính: 49,87 . 1000,16
Ta ước lượng 49,87 . 1000,16 \( \approx \) 50 . 1000 = 50 000

Trong toán học, việc làm tròn và ước lượng đóng vai trò quan trọng trong việc đơn giản hóa các phép tính và đưa ra các kết quả gần đúng khi không cần độ chính xác tuyệt đối. Đối với học sinh lớp 7, việc nắm vững lý thuyết này là nền tảng để giải quyết các bài toán thực tế và phát triển tư duy logic.
Làm tròn số là quá trình thay thế một số bằng một số gần đúng hơn, có ít chữ số hơn. Mục đích của việc làm tròn là để đơn giản hóa số, làm cho nó dễ đọc và dễ sử dụng hơn. Có hai loại làm tròn phổ biến:
Quy tắc làm tròn:
Ước lượng kết quả là quá trình tìm một giá trị gần đúng cho kết quả của một phép tính. Ước lượng thường được sử dụng khi không cần độ chính xác tuyệt đối hoặc khi việc tính toán chính xác là khó khăn.
Cách ước lượng kết quả:
Làm tròn và ước lượng có nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức về lý thuyết làm tròn và ước lượng, hãy cùng làm một số bài tập sau:
Lý thuyết Làm tròn và Ước lượng Toán 7 Cánh diều là một phần quan trọng của chương trình học. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và phát triển tư duy logic. Hãy luyện tập thường xuyên để củng cố kiến thức và áp dụng vào thực tế.
| Số | Làm tròn đến hàng phần trăm |
|---|---|
| 12,3456 | 12,35 |
| 3,14159 | 3,14 |
| Bảng ví dụ làm tròn số | |