Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục I trang 88, 89 SGK Toán 7 tập 2 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi luôn cố gắng mang đến những bài giải chất lượng nhất, đáp ứng nhu cầu học tập của các em.
I. Trường hợp bằng nhau góc – cạnh – góc (g.c.g)
Cho hai tam giác ABC và A’B’C’ (Hình 57) có:\(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
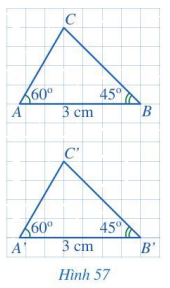
Phương pháp giải:
Đếm số ô vuông của cạnh BC và B’C’ rồi xem hai tam giác ABC và A’B’C’ có bằng nhau không.
Lời giải chi tiết:
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
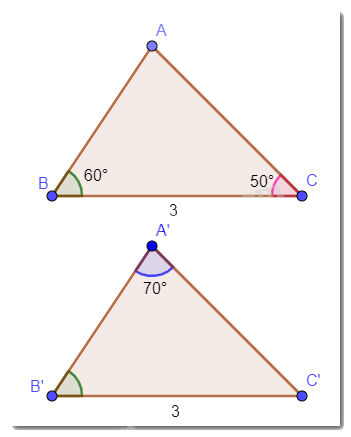
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Phương pháp giải:
Ta so sánh hai tam giác ABC và A’B’C’.
Lời giải chi tiết:
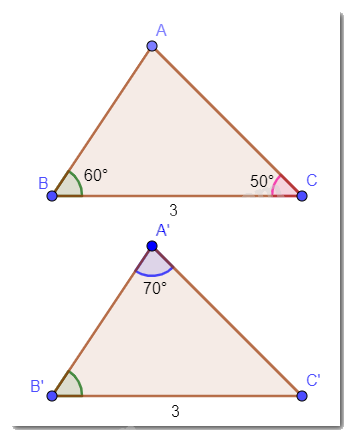
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Giải thích bài toán ở phần mở đầu.
Phương pháp giải:
Chứng minh tam giác ABC bằng tam giác ABD theo trường hợp góc cạnh góc.
Nếu một cạnh và hai góc liền kề cạnh đó của tam giác này bằng một cạnh và hai góc liền kề tương ứng của tam giác kia thì hai tam giác này bằng nhau.
Lời giải chi tiết:
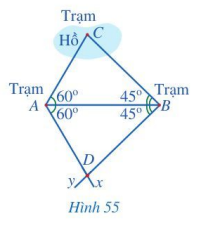
Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.
Vậy \(\Delta ABC = \Delta ABD\) (g.c.g).
Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)
I. Trường hợp bằng nhau góc – cạnh – góc (g.c.g)
Cho hai tam giác ABC và A’B’C’ (Hình 57) có:\(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
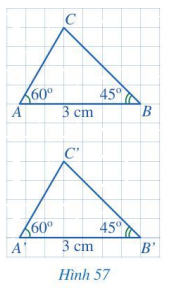
Phương pháp giải:
Đếm số ô vuông của cạnh BC và B’C’ rồi xem hai tam giác ABC và A’B’C’ có bằng nhau không.
Lời giải chi tiết:
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Phương pháp giải:
Ta so sánh hai tam giác ABC và A’B’C’.
Lời giải chi tiết:
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Giải thích bài toán ở phần mở đầu.
Phương pháp giải:
Chứng minh tam giác ABC bằng tam giác ABD theo trường hợp góc cạnh góc.
Nếu một cạnh và hai góc liền kề cạnh đó của tam giác này bằng một cạnh và hai góc liền kề tương ứng của tam giác kia thì hai tam giác này bằng nhau.
Lời giải chi tiết:
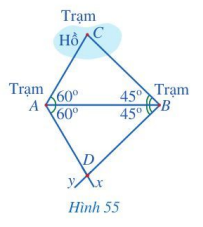
Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.
Vậy \(\Delta ABC = \Delta ABD\) (g.c.g).
Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)
Mục I trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải toán. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán lớp 7.
Bài tập mục I trang 88, 89 SGK Toán 7 tập 2 - Cánh diều bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các vấn đề cụ thể. Các dạng bài tập chính bao gồm:
Để thu gọn biểu thức, ta cần thực hiện các phép toán cộng, trừ, nhân, chia các đơn thức đồng dạng. Ví dụ, để thu gọn biểu thức 3x + 2x - 5x, ta thực hiện như sau:
3x + 2x - 5x = (3 + 2 - 5)x = 0x = 0
Để tính giá trị của biểu thức, ta thay các giá trị cụ thể của biến vào biểu thức và thực hiện các phép toán. Ví dụ, để tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2, ta thực hiện như sau:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Để chứng minh đẳng thức, ta cần biến đổi một vế của đẳng thức về dạng tương đương với vế còn lại. Ví dụ, để chứng minh đẳng thức (a + b)2 = a2 + 2ab + b2, ta thực hiện như sau:
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục I trang 88, 89 SGK Toán 7 tập 2 - Cánh diều trên giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán. Chúc các em học tốt!