Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trang 78 và 79 sách Toán 7 tập 2, chương trình Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng bắt đầu nhé!
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).
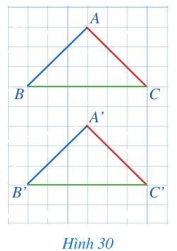
a) So sánh:
- Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.
- Các cặp góc: A và A’; B và B’; C và C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
c) Cắt mảnh giấy hình tam giác ABC và mảnh giất hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
Phương pháp giải:
a) Học sinh quan sát Hình 30 để so sánh các cặp cạnh và cặp góc.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không thì ta dựa vào mối liên hệ giữa các cặp cạnh và các cặp góc tương ứng của hai tam giác.
c) Học sinh tự thực hành cắt mảnh giấy để đưa ra kết luận.
Lời giải chi tiết:
a) AB = A’B’; BC = B’C’; CA = C’A’.
A = A’; B = B’; C = C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
Phương pháp giải:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
Lời giải chi tiết:
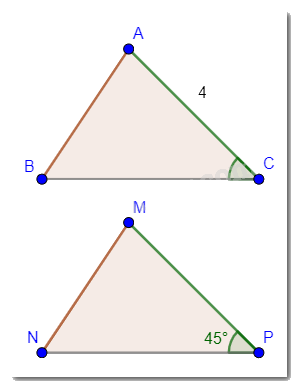
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).
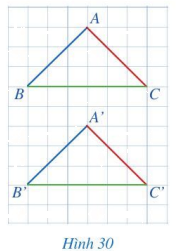
a) So sánh:
- Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.
- Các cặp góc: A và A’; B và B’; C và C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
c) Cắt mảnh giấy hình tam giác ABC và mảnh giất hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
Phương pháp giải:
a) Học sinh quan sát Hình 30 để so sánh các cặp cạnh và cặp góc.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không thì ta dựa vào mối liên hệ giữa các cặp cạnh và các cặp góc tương ứng của hai tam giác.
c) Học sinh tự thực hành cắt mảnh giấy để đưa ra kết luận.
Lời giải chi tiết:
a) AB = A’B’; BC = B’C’; CA = C’A’.
A = A’; B = B’; C = C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
Phương pháp giải:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
Lời giải chi tiết:
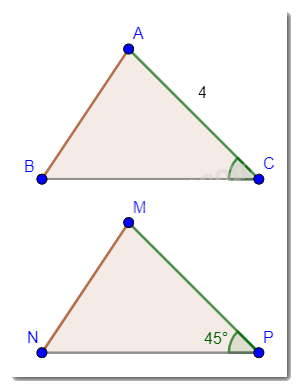
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
Trang 78 và 79 SGK Toán 7 tập 2 Cánh Diều tập trung vào các bài tập liên quan đến việc vận dụng các kiến thức đã học về tam giác, góc và các tính chất liên quan. Các bài tập thường yêu cầu học sinh phải phân tích đề bài, xác định các yếu tố cần tìm và áp dụng các định lý, tính chất đã học để giải quyết vấn đề.
Bài 1 thường yêu cầu học sinh vẽ hình và xác định các yếu tố của tam giác dựa trên các thông tin đã cho. Ví dụ, cho một tam giác ABC với các điều kiện về độ dài cạnh, số đo góc, yêu cầu học sinh vẽ tam giác và xác định các yếu tố còn lại.
Bài 2 thường liên quan đến việc tính toán các góc của tam giác. Học sinh cần áp dụng định lý tổng ba góc trong một tam giác để tính toán góc còn lại khi biết hai góc. Ngoài ra, bài tập có thể yêu cầu học sinh chứng minh các mối quan hệ giữa các góc trong tam giác.
Bài 3 thường là các bài tập ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức về tam giác để giải quyết các vấn đề trong đời sống. Ví dụ, tính chiều cao của một ngọn cây dựa trên số đo góc và khoảng cách từ người quan sát đến gốc cây.
Bài 4 thường là các bài tập nâng cao, yêu cầu học sinh phải suy luận logic và vận dụng linh hoạt các kiến thức đã học. Bài tập có thể yêu cầu học sinh chứng minh các tính chất của tam giác hoặc giải các bài toán phức tạp hơn.
Để giúp các em giải bài tập một cách hiệu quả, giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập. Lời giải bao gồm các bước giải rõ ràng, dễ hiểu, cùng với các giải thích cụ thể về lý do tại sao lại thực hiện các bước đó. Các em có thể tham khảo lời giải để hiểu rõ hơn về cách giải bài tập và tự mình giải các bài tập tương tự.
Ví dụ: Cho tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc C.
Giải:
Áp dụng định lý tổng ba góc trong một tam giác, ta có:
Góc A + Góc B + Góc C = 180 độ
60 độ + 80 độ + Góc C = 180 độ
Góc C = 180 độ - 60 độ - 80 độ
Góc C = 40 độ
Ngoài SGK Toán 7 tập 2 Cánh Diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trang 78, 79 SGK Toán 7 tập 2 Cánh Diều, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán. Chúc các em thành công!