Chào mừng bạn đến với bài học về Lý thuyết Tia phân giác của một góc trong chương trình Toán 7 Cánh Diều. Đây là một khái niệm quan trọng, đặt nền móng cho các kiến thức hình học nâng cao hơn. Bài viết này sẽ cung cấp cho bạn một cách tiếp cận toàn diện, từ định nghĩa, tính chất đến ứng dụng thực tế.
Chúng ta sẽ cùng nhau khám phá cách xác định tia phân giác, các tính chất đặc biệt của nó và cách sử dụng lý thuyết này để giải các bài toán hình học một cách hiệu quả.
I. Định nghĩa Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
I. Định nghĩa
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Ví dụ:
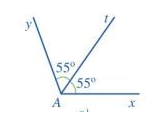
Tia At là tia phân giác của góc xAy vì tia At nằm trong góc xAy và \(\widehat {xAt} = \widehat {yAt}( = 55^\circ )\)
Chú ý:
Ta cũng có thể hiểu Om là tia phân giác của góc xOy \( \Leftrightarrow \widehat {xOm} = \widehat {yOm} = \frac{1}{2}\widehat {xOy}\)
II. Vẽ tia phân giác của một góc
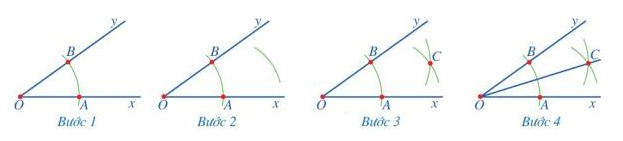
Cách 1: Dùng compa
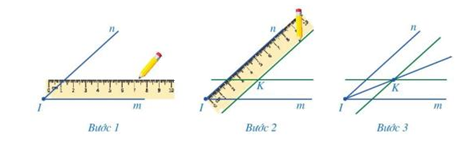
Cách 2: Dùng thước thẳng
Trong hình học, góc là một khái niệm cơ bản, và tia phân giác đóng vai trò quan trọng trong việc chia một góc thành hai góc bằng nhau. Bài viết này sẽ trình bày chi tiết về lý thuyết tia phân giác của một góc theo chương trình SGK Toán 7 Cánh Diều, bao gồm định nghĩa, tính chất và ứng dụng.
Định nghĩa: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh đó hai góc bằng nhau.
Ví dụ: Cho góc ∠AOB. Tia OC được gọi là tia phân giác của ∠AOB nếu OC nằm giữa OA và OB, và ∠AOC = ∠BOC.
Tính chất 1: Nếu một tia là tia phân giác của một góc thì tia đó tạo với mỗi cạnh của góc một góc bằng nửa góc đó.
Ví dụ: Nếu OC là tia phân giác của ∠AOB thì ∠AOC = ∠BOC = ∠AOB / 2.
Tính chất 2: Ngược lại, nếu một tia nằm giữa hai cạnh của một góc và tạo với mỗi cạnh một góc bằng nửa góc đó thì tia đó là tia phân giác của góc đó.
Ví dụ: Nếu OC nằm giữa OA và OB, và ∠AOC = ∠BOC = ∠AOB / 2 thì OC là tia phân giác của ∠AOB.
Có nhiều cách để xác định tia phân giác của một góc:
Lý thuyết tia phân giác của một góc có nhiều ứng dụng trong hình học, đặc biệt là trong việc giải các bài toán liên quan đến tam giác cân, tam giác đều và các bài toán chứng minh tính chất hình học.
Bài tập 1: Cho góc ∠ABC = 60°. Vẽ tia phân giác BD của góc ∠ABC. Tính số đo của góc ∠ABD.
Giải: Vì BD là tia phân giác của ∠ABC nên ∠ABD = ∠CBD = ∠ABC / 2 = 60° / 2 = 30°.
Bài tập 2: Cho tam giác ABC cân tại A. Vẽ tia phân giác AD của góc ∠BAC. Chứng minh rằng AD là đường cao của tam giác ABC.
Giải: Vì AD là tia phân giác của ∠BAC và tam giác ABC cân tại A nên ∠BAD = ∠CAD. Xét hai tam giác ABD và ACD, ta có:
Do đó, ΔABD = ΔACD (c.g.c). Suy ra ∠ADB = ∠ADC. Vì ∠ADB + ∠ADC = 180° nên ∠ADB = ∠ADC = 90°. Vậy AD là đường cao của tam giác ABC.
Khi làm bài tập về tia phân giác, cần chú ý:
Lý thuyết tia phân giác của một góc là một kiến thức quan trọng trong chương trình Toán 7. Việc nắm vững định nghĩa, tính chất và ứng dụng của tia phân giác sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và tự tin hơn. Chúc bạn học tốt!