Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục I trang 100 và 101 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
I. Định nghĩa
Quan sát Hình 87.
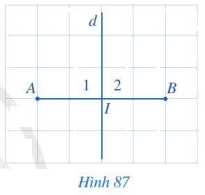
a) So sánh hai đoạn thẳng IA và IB.
b) Tìm số đo của các góc \({I_1},{I_2}\).
Phương pháp giải:
a) Đếm số ô vuông để xác định độ dài đoạn thẳng IA, IB.
b) Quan sát Hình 87 để đưa ra số đo góc của các góc \({I_1},{I_2}\) .
Lời giải chi tiết:
a) \(IA = IB = 2\).
b) \({I_1} = {I_2} = 90^\circ \).
Cho tam giác ABC và M là trung điểm của BC. Biết \(\widehat {AMB} = \widehat {AMC}\). Chứng minh AM là đường trung trực của đoạn thẳng BC.
Phương pháp giải:
Chứng minh AM đi qua trung điểm của đoạn thẳng BC và vuông góc với đoạn thẳng BC
Lời giải chi tiết:
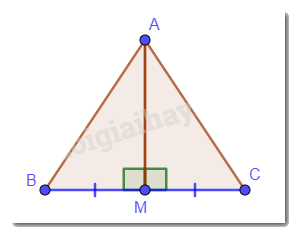
M là trung điểm của BC nên B, M, C thằng hàng → \(\widehat {BMC} = 180^\circ \). Mà \(\widehat {AMB} = \widehat {AMC}\)nên \(\widehat {AMB} = \widehat {AMC} = 180^\circ :2 = 90^\circ \)→ \(AM \bot BC\).
Vậy AM đi qua trung điểm M của đoạn thẳng BC và AM vuông góc với BC. Hay AM là đường trung trực của đoạn thẳng BC.
I. Định nghĩa
Quan sát Hình 87.
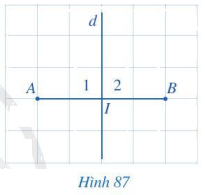
a) So sánh hai đoạn thẳng IA và IB.
b) Tìm số đo của các góc \({I_1},{I_2}\).
Phương pháp giải:
a) Đếm số ô vuông để xác định độ dài đoạn thẳng IA, IB.
b) Quan sát Hình 87 để đưa ra số đo góc của các góc \({I_1},{I_2}\) .
Lời giải chi tiết:
a) \(IA = IB = 2\).
b) \({I_1} = {I_2} = 90^\circ \).
Cho tam giác ABC và M là trung điểm của BC. Biết \(\widehat {AMB} = \widehat {AMC}\). Chứng minh AM là đường trung trực của đoạn thẳng BC.
Phương pháp giải:
Chứng minh AM đi qua trung điểm của đoạn thẳng BC và vuông góc với đoạn thẳng BC
Lời giải chi tiết:
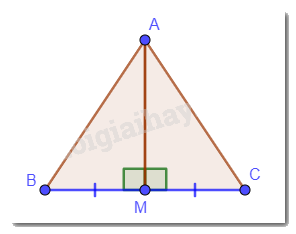
M là trung điểm của BC nên B, M, C thằng hàng → \(\widehat {BMC} = 180^\circ \). Mà \(\widehat {AMB} = \widehat {AMC}\)nên \(\widehat {AMB} = \widehat {AMC} = 180^\circ :2 = 90^\circ \)→ \(AM \bot BC\).
Vậy AM đi qua trung điểm M của đoạn thẳng BC và AM vuông góc với BC. Hay AM là đường trung trực của đoạn thẳng BC.
Mục I trong SGK Toán 7 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể, thường là các kiến thức về tam giác, góc, hoặc các phép biến hình. Việc nắm vững lý thuyết và phương pháp giải bài tập trong mục này là nền tảng quan trọng để học tốt các kiến thức tiếp theo.
Để hiểu rõ hơn về Mục I trang 100, 101, chúng ta cần xem xét các nội dung chính sau:
Để giải các bài tập trong Mục I trang 100, 101 một cách hiệu quả, các em có thể áp dụng các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục I trang 100, 101 SGK Toán 7 tập 2 - Cánh diều:
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước)
Để hiểu sâu hơn về chủ đề trong Mục I, các em có thể tham khảo thêm các tài liệu sau:
Việc luyện tập thường xuyên và áp dụng kiến thức vào thực tế là cách tốt nhất để học tốt môn Toán. Chúc các em học tập tốt!