Chào mừng các em học sinh đến với lời giải chi tiết bài 12 trang 120 SGK Toán 7 tập 2 - Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh giải quyết các bài tập toán một cách hiệu quả nhất.
Cho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc nào sau đây? A. Góc HPN. B. Góc NMP. C. Góc MPN. D. Góc NHP.
Đề bài
Cho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc nào sau đây?
A. Góc HPN.
B. Góc NMP.
C. Góc MPN.
D. Góc NHP.
Phương pháp giải - Xem chi tiết
Gọi D, E lần lượt là chân đường cao kẻ từ H đến MN và NP.
Sử dụng tính chất về tổng các góc trong tam giác vuông: trong tam giác vuông, tổng hai góc nhọn bằng \(90^\circ \) cho tam giác MDH và PEH.
Kết hợp tính chất của hai góc đối đỉnh thì bằng nhau.
Lời giải chi tiết
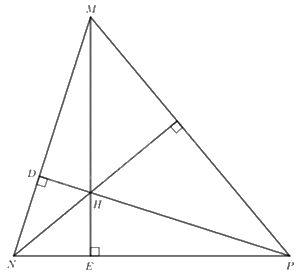
Gọi D, E lần lượt là chân đường cao kẻ từ H đến MN và NP.
Xét tam giác MDH vuông tại D, ta có: \(\widehat {HMD} + \widehat {MHD} = 90^\circ \) (tổng hai góc nhọn trong tam giác vuông)
Suy ra \(\widehat {HMD} = 90^\circ - \widehat {MHD}\)
Xét tam giác PEH vuông tại E, ta có: \(\widehat {HPE} + \widehat {PHE} = 90^\circ \) (tổng hai góc nhọn trong tam giác vuông)
Suy ra \(\widehat {HPE} = 90^\circ - \widehat {PHE}\)
Mà \(\widehat {MHD} = \widehat {PHE}\) (hai góc đối đỉnh)
Do đó \(\widehat {HMD} = \widehat {HPE}\) hay \(\widehat {HMN} = \widehat {HPN}\).
Đáp án A
Bài 12 trang 120 SGK Toán 7 tập 2 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về tam giác cân, tính chất đường trung tuyến trong tam giác, và các định lý liên quan đến góc trong tam giác. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp chứng minh hình học.
Bài tập 12 yêu cầu học sinh chứng minh một số tính chất liên quan đến tam giác cân và đường trung tuyến. Cụ thể, bài tập thường xoay quanh việc chứng minh hai tam giác bằng nhau, từ đó suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau. Để giải bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho bài tập 12 trang 120 SGK Toán 7 tập 2 - Cánh diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các hình vẽ minh họa để giúp các em hình dung rõ hơn về bài toán.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Sau đó, chúng ta cần phân tích các yếu tố đã cho và tìm ra mối liên hệ giữa chúng. Từ đó, chúng ta có thể đưa ra hướng giải phù hợp.
Sau khi đã có hướng giải, chúng ta tiến hành thực hiện chứng minh và giải bài tập. Trong quá trình giải, chúng ta cần trình bày các bước giải một cách logic và rõ ràng, sử dụng các ký hiệu toán học chính xác. Đồng thời, chúng ta cần giải thích rõ ràng các bước giải để người đọc có thể hiểu được.
Sau khi đã giải xong bài tập, chúng ta cần kiểm tra lại kết quả để đảm bảo tính chính xác. Nếu kết quả đúng, chúng ta có thể rút ra kết luận và ghi lại vào vở. Nếu kết quả sai, chúng ta cần xem lại các bước giải và tìm ra lỗi sai để sửa chữa.
Để giúp các em hiểu rõ hơn về cách giải bài tập 12, chúng ta sẽ xem xét một ví dụ minh họa cụ thể. Ví dụ này sẽ giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Sau khi đã học xong bài 12, các em có thể làm thêm một số bài tập tương tự để củng cố kiến thức và rèn luyện kỹ năng. Chúng tôi sẽ cung cấp một số bài tập tham khảo để các em luyện tập.
Khi giải các bài tập về tam giác cân và đường trung tuyến, các em cần lưu ý một số điều sau:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải quyết bài tập 12 trang 120 SGK Toán 7 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!