Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục III trang 94 và 95 sách giáo khoa Toán 7 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
III. Dấu hiệu nhận biết
Cho tam giác ABC thỏa mãn \(\widehat B = \widehat C\). Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).
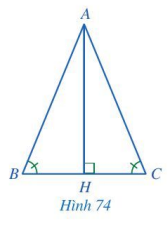
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?
b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?
Phương pháp giải:
a) Xét hai tam giác BAH và CAH theo trường hợp g.c.g.
b) Sử dụng kết quả phần a) để xét hai cạnh AB và AC. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau
Lời giải chi tiết:
a) \(\widehat B = \widehat C\). Mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat {BAH} = \widehat {CAH}\).
Xét hai tam giác BAH và CAH có:
\(\widehat {BAH} = \widehat {CAH}\);
AH chung;
\(\widehat {AHB} = \widehat {AHC}\) (= 90°).
Vậy \(\Delta BAH = \Delta CAH\)(g.c.g)
b) \(\Delta BAH = \Delta CAH\) nên AB = AC ( 2 cạnh tương ứng).
III. Dấu hiệu nhận biết
Cho tam giác ABC thỏa mãn \(\widehat B = \widehat C\). Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).
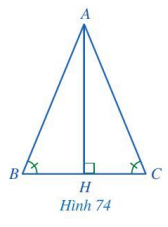
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?
b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?
Phương pháp giải:
a) Xét hai tam giác BAH và CAH theo trường hợp g.c.g.
b) Sử dụng kết quả phần a) để xét hai cạnh AB và AC. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau
Lời giải chi tiết:
a) \(\widehat B = \widehat C\). Mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat {BAH} = \widehat {CAH}\).
Xét hai tam giác BAH và CAH có:
\(\widehat {BAH} = \widehat {CAH}\);
AH chung;
\(\widehat {AHB} = \widehat {AHC}\) (= 90°).
Vậy \(\Delta BAH = \Delta CAH\)(g.c.g)
b) \(\Delta BAH = \Delta CAH\) nên AB = AC ( 2 cạnh tương ứng).
Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.
Phương pháp giải:
Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.
Lời giải chi tiết:
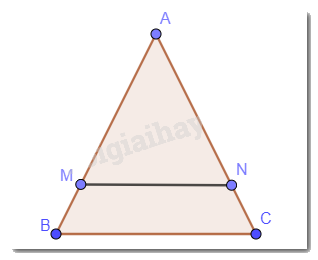
Ta có tam giác ABC cân mà MN // BC. Nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\)(đồng vị)
Mà \(\widehat {ABC} = \widehat {ACB}\)(tam giác ABC cân) nên \(\widehat {AMN} = \widehat {ANM}\).
Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)
Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.
Phương pháp giải:
Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.
Lời giải chi tiết:
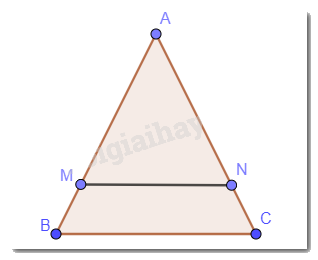
Ta có tam giác ABC cân mà MN // BC. Nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\)(đồng vị)
Mà \(\widehat {ABC} = \widehat {ACB}\)(tam giác ABC cân) nên \(\widehat {AMN} = \widehat {ANM}\).
Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)
Mục III trong SGK Toán 7 tập 2 - Cánh diều tập trung vào việc ôn tập chương và chuẩn bị cho kiểm tra cuối kỳ. Các bài tập trong mục này thường bao gồm các dạng bài tập tổng hợp từ các chủ đề đã học, đòi hỏi học sinh phải vận dụng linh hoạt kiến thức và kỹ năng đã được trang bị.
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ, đồng thời vận dụng các tính chất của phép toán để đơn giản hóa biểu thức. Việc nắm vững các quy tắc dấu và thứ tự thực hiện phép toán là rất quan trọng để giải quyết bài tập này một cách chính xác.
Bài tập này tập trung vào việc nhận biết và giải các bài toán liên quan đến tỉ lệ thức. Học sinh cần hiểu rõ định nghĩa tỉ lệ thức, tính chất của tỉ lệ thức và cách áp dụng chúng để giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại góc (góc nhọn, góc tù, góc vuông), các cặp góc so le trong, đồng vị, trong cùng phía và tính chất của đường thẳng song song để giải quyết các bài toán liên quan đến hình học.
| Loại góc | Định nghĩa |
|---|---|
| Góc nhọn | Góc có số đo nhỏ hơn 90 độ |
| Góc tù | Góc có số đo lớn hơn 90 độ và nhỏ hơn 180 độ |
| Góc vuông | Góc có số đo bằng 90 độ |
Để giải các bài tập trong mục III trang 94, 95 SGK Toán 7 tập 2 - Cánh diều một cách hiệu quả, học sinh cần:
Trong quá trình giải bài tập, học sinh cần chú ý:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất trong môn Toán 7.