Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 2 trang 103 SGK Toán 7 tập 2 - Cánh diều. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự. Hãy cùng theo dõi!
Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:
Đề bài
Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:
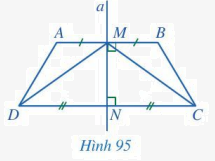
a) AB // CD;
b) \(\Delta MNC = \Delta MND;\)
c) \(\widehat {AMD} = \widehat {BMC}\);
d) \(AD = BC,\widehat A = \widehat B\);
e) \(\widehat {ADC} = \widehat {BCD}\).
Phương pháp giải - Xem chi tiết
a) Chứng minh AB // CD bằng cách dựa vào đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.
b) Chứng minh \(\Delta MNC = \Delta MND\) theo trường hợp cạnh huyền – cạnh góc vuông.
c) Dựa vào kết quả của phần b) để chứng minh \(\widehat {AMD} = \widehat {BMC}\).
d) Chứng minh \(AD = BC,\widehat A = \widehat B\) dựa vào cách chứng minh \(\Delta MAD = \Delta MBC\).
e) Chứng minh \(\widehat {ADC} = \widehat {BCD}\) dựa vào kết quả của phần d).
Lời giải chi tiết
a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).
Bài 2 trang 103 SGK Toán 7 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán liên quan đến góc so le trong, góc đồng vị, góc trong cùng phía. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và tính chất sau:
Để giải bài 2 trang 103 SGK Toán 7 tập 2 - Cánh diều, chúng ta cần phân tích đề bài và xác định các góc cần tính. Sau đó, vận dụng các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để tìm ra mối liên hệ giữa các góc và tính toán giá trị của chúng.
Ví dụ, nếu đề bài cho biết góc A bằng 60 độ và yêu cầu tính góc B, ta có thể sử dụng tính chất góc so le trong hoặc góc đồng vị để suy ra góc B cũng bằng 60 độ. Hoặc, nếu đề bài cho biết góc A và góc B là hai góc trong cùng phía, ta có thể sử dụng tính chất góc trong cùng phía bù nhau để suy ra góc B bằng 180 độ trừ đi góc A.
Để củng cố kiến thức và kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, học sinh có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Dưới đây là một số bài tập gợi ý:
Để giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song một cách hiệu quả, học sinh nên:
Bài 2 trang 103 SGK Toán 7 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ và vận dụng các kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.