Chào mừng các em học sinh đến với bài giải chi tiết bài tập 1.10 trang 14 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\)trên nửa khoảng \([2;6)\) d) \(y = f(x) = \sqrt {4 - {x^2}} \) e) \(y = f(x) = {e^x} - x\)trên đoạn \([ - 1;2]\) f) \(y = f(x) = x\ln x\)trên đoạn \([{e^{ - 2}};e]\)
Đề bài
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau
a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\)
b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\)
c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\)
d) \(y = f(x) = \sqrt {4 - {x^2}} \)
e) \(y = f(x) = {e^x} - x\) trên đoạn \([ - 1;2]\)
f) \(y = f(x) = x\ln x\) trên đoạn \([{e^{ - 2}};e]\)
Phương pháp giải - Xem chi tiết
Bước 1 Tính \(f'(x)\)
Bước 2 Lập bảng biến thiên
Bước 3 Tìm cực trị của hàm số trên đoạn
Bước 4 Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số trên các khoảng
Lời giải chi tiết
a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\)
Hàm số trên xác định trên R
Ta có \(f'(x) = {x^2} + 4x + 3\)
Xét \(f'(x) = 0\)
\( \Rightarrow {x^2} + 4x + 3 = 0\) \( \Rightarrow \left[ \begin{array}{l}x = - 1\\x = - 3\end{array} \right.\)
Ta có bảng biến thiên
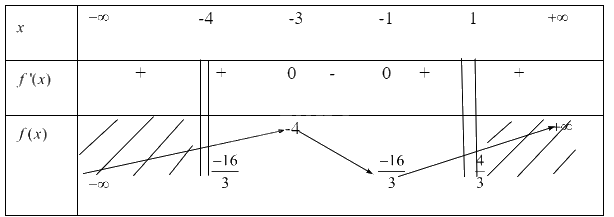
Từ bảng biến thiên ta có
Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTLN trên đoạn \([ - 4;1]\) tại x = 1 khi đó y = \(\frac{4}{3}\)
Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTNN trên đoạn \([ - 4;1]\) tại x = -4 và x= -1 khi đó y = \(\frac{{ - 16}}{3}\)
b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\)
Hàm số trên xác định trên R/{0}
Ta có \(f'(x) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\)
Xét \(f'(x) = 0\)
\( \Rightarrow {x^2} - 1 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Ta có bảng biến thiên
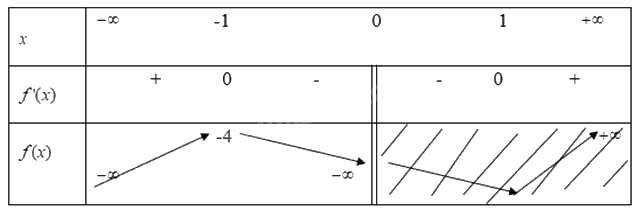
Vậy hàm số \(y = f(x) = x + \frac{1}{x} - 2\) đạt GTLN trên khoảng \(( - \infty ;0)\) tại x=-1 khi đó y=-4
c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\)
Hàm số xác định trên R/\(\left\{ {\frac{3}{2}} \right\}\)
Ta có \(f'(x) = \frac{1}{{{{(2x - 3)}^2}}}\)
Vì \(f'(x) > 0\) với \(x \in R/\left\{ {\frac{3}{2}} \right\}\)
Nên hàm số luôn đồng biến với \(x \in R/\left\{ {\frac{3}{2}} \right\}\)
Khi đó ta có bảng biến thiên
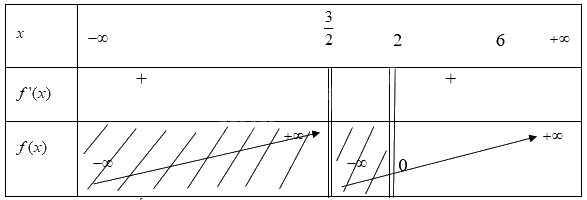
Từ bảng biến thiên ta có:
Hàm số \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) đạt GTNN trên nửa khoảng \([2;6)\) tại x = 2 khi đó y = 0
d) \(y = f(x) = \sqrt {4 - {x^2}} \)
Hàm số xác định với \(\begin{array}{l}x \in [ - 2;2]\\\end{array}\)
Ta có \(f'(x) = \frac{{ - 2x}}{{2\sqrt {4 - {x^2}} }}\)
Xét \(f'(x) = 0\)\( \Rightarrow x = 0\)
Từ đó ta có bảng biến thiên
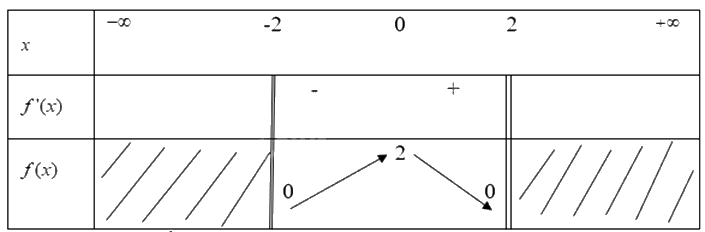
Từ bảng biến thiên, ta có:
Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTLN tại x = 0 khi đó y =2
Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTNN tại x = 2 và x= -2 khi đó y =2
e) \(y = f(x) = {e^x} - x\) trên khoảng \([ - 1;2]\)
Hàm số xác định trên R
Ta có \(f'(x) = {e^x} - 1\)
Xét \(f'(x) = 0\)
\( \Rightarrow {e^x} - 1 = 0\)
\( \Rightarrow x = 0\)
Từ đó ta có bảng biến thiên
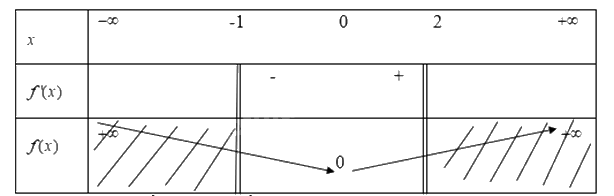
Từ bảng biến thiên ta thấy
Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=0 khi đó y=0
Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=2 khi đó y=5,9
f) \(y = f(x) = x\ln x\) trên khoảng \([{e^{ - 2}};e]\)
Hàm số trên xác định với \(x \in \left( {0; + \infty } \right)\)
Ta có \(f'(x) = \ln x + 1\)
Xét \(f'(x) = \ln x + 1\) \( \Rightarrow x = {e^{ - 1}}\)
Từ đó ta có bảng biến thiên là
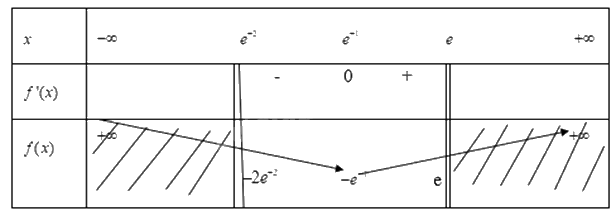
Từ bảng biến thiên ta có:
Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x=e khi đó y=e
Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x= \({e^{ - 1}}\) khi đó y= \( - {e^{ - 1}}\)
Bài tập 1.10 trang 14 SGK Toán 12 tập 1 yêu cầu tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Giới hạn của hàm số f(x) khi x tiến tới a, ký hiệu là limx→a f(x), là giá trị mà f(x) tiến tới khi x càng gần a nhưng không bằng a. Để tính giới hạn, chúng ta có thể sử dụng các phương pháp sau:
Để giải bài tập 1.10 trang 14 SGK Toán 12 tập 1, chúng ta cần xác định hàm số và giá trị x mà chúng ta cần tính giới hạn. Sau đó, áp dụng một trong các phương pháp trên để tính giới hạn.
Ví dụ, giả sử bài tập 1.10 có dạng:
limx→2 (x2 - 4) / (x - 2)
Chúng ta có thể giải bài tập này như sau:
Ngoài bài tập 1.10, còn rất nhiều dạng bài tập giới hạn hàm số khác mà các em có thể gặp phải. Dưới đây là một số dạng bài tập thường gặp:
Để giải bài tập giới hạn hàm số một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Để củng cố kiến thức về giới hạn hàm số, các em có thể tự giải thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng bài giải chi tiết bài tập 1.10 trang 14 SGK Toán 12 tập 1 này sẽ giúp các em hiểu rõ hơn về giới hạn hàm số và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!