Chào mừng các em học sinh đến với bài giải bài tập 3.13 trang 104 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Một công ty giống cây trồng đã thử nghiệm hai phương pháp chăm sóc khác nhau cho cây hướng dương. Sau hai tuần, người ta thấy cây được chăm sóc theo cả hai phương pháp đều thấp hơn 50 cm. Hình 3.5a và 3.5b biểu diễn chiều cao của một số cây.
Đề bài
Một công ty giống cây trồng đã thử nghiệm hai phương pháp chăm sóc khác nhau cho cây hướng dương. Sau hai tuần, người ta thấy cây được chăm sóc theo cả hai phương pháp đều thấp hơn 50 cm. Hình 3.5a và 3.5b biểu diễn chiều cao của một số cây.
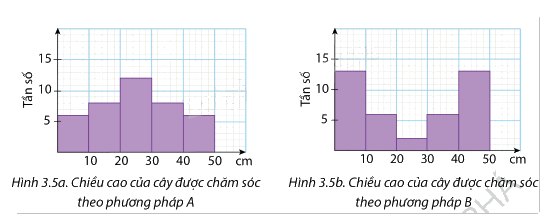
a) Ước tính số trung bình và độ lệch chuẩn của chiều cao các cây được chăm sóc theo mỗi phương pháp.
b) So sánh hiệu quả của các phương pháp trên hai phương diện:
- Chiều cao trung bình của cây.
- Sự đồng đều về chiều cao của cây.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức sau:
- Công thức tính trung bình:
\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)
b)
- So sánh giá trị trung bình của hai phương pháp để đánh giá chiều cao trung bình của cây.
- So sánh độ lệch chuẩn của hai phương pháp để đánh giá sự đồng đều về chiều cao của cây.
Lời giải chi tiết
a) Bảng phân phối tần số cho phương pháp A và B:
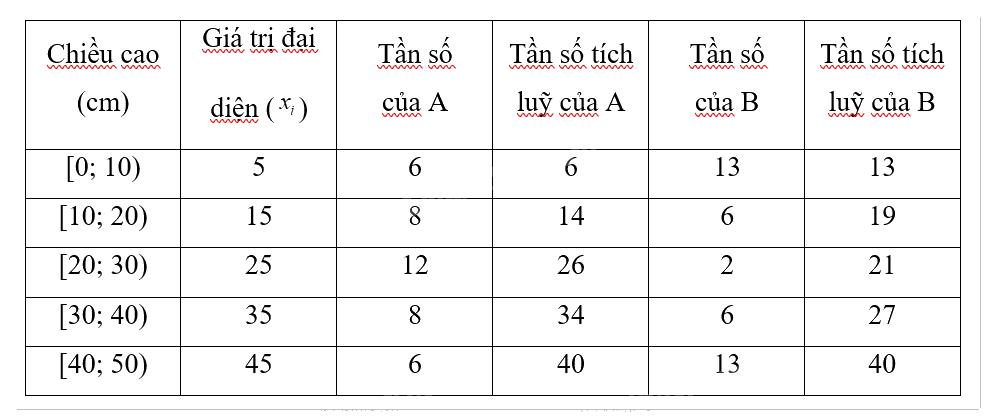
Dựa vào bảng phân phối ta thấy N = 40
Giá trị trung bình của phương pháp A:
\({\bar x_A} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{6 \times 5 + 8 \times 15 + 12 \times 25 + 8 \times 35 + 6 \times 45}}{{40}} = 25cm\)
Độ lệch chuẩn của phương pháp A:
\({S_A} = \sqrt {\frac{1}{{40}}\sum\limits_{i = 1}^5 {{f_i}} \times {{({x_i} - 25)}^2}} \)
\({S_A} = \sqrt {\frac{{6 \times {{(5 - 25)}^2} + 8 \times {{(15 - 25)}^2} + 12 \times {{(25 - 25)}^2} + 8 \times {{(35 - 25)}^2} + 6 \times {{(45 - 25)}^2}}}{{40}}} \)
\({S_A} = \sqrt {160} = 4\sqrt {10} \approx 12,65cm\)
Giá trị trung bình của phương pháp B:
\({\bar x_B} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{13 \times 5 + 6 \times 15 + 2 \times 25 + 6 \times 35 + 13 \times 45}}{{40}} = 25cm\)
Độ lệch chuẩn của phương pháp B:
\({S_B} = \sqrt {\frac{1}{{40}}\sum\limits_{i = 1}^5 {{f_i}} \times {{({x_i} - 25)}^2}} \)
\({S_B} = \sqrt {\frac{{13 \times {{(5 - 25)}^2} + 6 \times {{(15 - 25)}^2} + 2 \times {{(25 - 25)}^2} + 6 \times {{(35 - 25)}^2} + 13 \times {{(45 - 25)}^2}}}{{40}}} \)
\({S_B} = \sqrt {290} \approx 17,03cm\)
b)
- Chiều cao trung bình: Cả hai phương pháp có cùng số trung bình là 25 cm, cho thấy rằng chiều cao trung bình của các cây là như nhau trong cả hai phương pháp chăm sóc.
- Sự đồng đều về chiều cao của cây: Phương pháp A có độ lệch chuẩn nhỏ hơn (12.65 cm) so với phương pháp B (17.03 cm), chỉ ra rằng cây trong phương pháp A có sự đồng đều về chiều cao hơn so với cây trong phương pháp B.
Bài tập 3.13 trang 104 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị và khảo sát hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức liên quan đến đạo hàm.
Đề bài thường yêu cầu tìm cực trị của hàm số hoặc khảo sát sự biến thiên của hàm số. Ví dụ, một đề bài có thể như sau: Cho hàm số y = f(x). Tìm các điểm cực trị của hàm số và vẽ đồ thị hàm số.
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Kết luận: Hàm số y = x3 - 3x2 + 2 có điểm cực đại là (0; 2) và điểm cực tiểu là (2; -2).
Để nắm vững phương pháp giải bài tập về đạo hàm và cực trị, các em nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi giải các bài toán khó.