Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 97, 98, 99 SGK Toán 12 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II". a) Hoàn thành sơ đồ hình cây sau:
Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 12 Cùng khám phá
Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.
Phương pháp giải:
- Sử dụng công thức xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\)
- Xác định tỉ lệ dân số nam và nữ
- Biết tỉ lệ mắc bệnh của từng giới
- Giải phương trình để tìm tỉ lệ nam mắc bệnh
Lời giải chi tiết:
* Xác định các biến cố:
\(A\): Biến cố là nam giới
\(B\): Biến cố là nữ giới
\(C\): Biến cố mắc bệnh bạch tạng
* Theo đề bài ta có các xác suất
\(P(A) = \frac{2}{5}\) ,\(P(B) = \frac{3}{5}\) ,\(P(C) = 0,45\% \),\(P(C|B) = 0,35\% \)
* Áp dụng công thức toàn phần
\(P(C) = P(A) \cdot P(C|A) + P(B) \cdot P(C|B)\)
\(0,45\% = (\frac{2}{5} \cdot P(C|A)) + (\frac{3}{5} \cdot 0,35\% )\)
* Giải Phương Trình
\(0,45\% = \frac{2}{5} \cdot P(C|A) + 0,21\% \)
\(0,45\% - 0,21\% = \frac{2}{5} \cdot P(C|A)\)
\(0,24\% = \frac{2}{5} \cdot P(C|A)\)
* Tính Tỉ Lệ Nam Mắc Bệnh
\(P(C|A) = \frac{{0,24\% \cdot 5}}{2}\)
\(P(C|A) = 0,6\% \)
Vậy tỉ lệ nam giới mắc bệnh bạch tạng là \(0,6\% \)
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.
Phương pháp giải:
Sử dụng công thức tính xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\).
Lời giải chi tiết:
* Các biến cố:
\(A\): Biến cố lấy quả trắng lần đầu
\(\bar A\): Biến cố lấy quả đen lần đầu
\(B\): Biến cố lấy quả trắng lần thứ hai
Xác suất ban đầu:
\(P(A) = \frac{5}{{15}} = \frac{1}{3}\)
\(P(\bar A) = \frac{{10}}{{15}} = \frac{2}{3}\)
* Xác suất có điều kiện:
\(P(B|A) = \frac{4}{{14}} = \frac{2}{7}\)
\(P(B|\bar A) = \frac{5}{{14}}\)
* Công thức xác suất toàn phần: \(P(B) = P(A) \cdot P(B|A) + P(\bar A) \cdot P(B|\bar A)\)
Thay số: \(P(B) = \left( {\frac{1}{3} \cdot \frac{2}{7}} \right) + \left( {\frac{2}{3} \cdot \frac{5}{{14}}} \right) = \frac{2}{{21}} + \frac{{10}}{{42}} = \frac{2}{{21}} + \frac{5}{{21}} = \frac{7}{{21}} = \frac{1}{3}\)
Vậy xác suất lấy được quả cầu trắng lần thứ hai là: \(P(B) = \frac{1}{3}\)
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cùng khám phá
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II".
a) Hoàn thành sơ đồ hình cây sau:
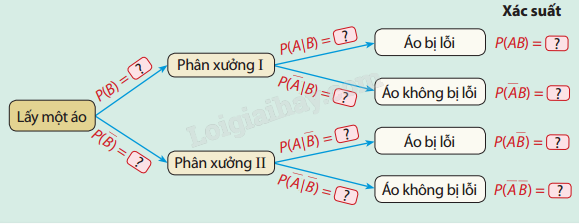
b) Ta nhận thấy biến cố A: "Lấy được áo bị lỗi" có thể xảy ra đồng thời với biến cố B: "Áo được sản xuất bởi phân xưởng I" hoặc biến cố B: "Áo được sản xuất bởi phân xưởng II". Người ta chứng minh được rằng: \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\). Hãy tính xác suất lấy được áo bị lỗi trong lô hàng.
Phương pháp giải:
a) Sử dụng công thức \(P(B|A) = \frac{{P(AB)}}{{P(A)}}\) hoặc \(P(AB) = P(B|A).P(A)\).
b) Sử dụng kết quả ở câu a và áp dụng công thức \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\) để tính xác suất.
Lời giải chi tiết:
a)
- Xác suất phân xưởng I sản xuất áo: \(P(B) = 0,4\)
- Xác suất phân xưởng II sản xuất áo: \(P(\bar B) = 0,6\)
- Xác suất áo bị lỗi từ phân xưởng I: \(P(A|B) = 0,02\)
- Xác suất áo bị lỗi từ phân xưởng II: \(P(A|\bar B) = 0.03\)
- Xác suất áo không bị lỗi từ phân xưởng I và phân xưởng II
Áo không bị lỗi từ phân xưởng I: \(P(\bar A|B) = 1 - P(A|B) \Leftrightarrow P(\bar A|B) = 1 - 0,02 = 0,98\)
Áo không bị lỗi từ phân xưởng II: \(P(\bar A|\bar B) = 1 - P(A|\bar B) \Leftrightarrow P(\bar A|\bar B) = 1 - 0.03 = 0,97\)
- Xác suất \(P(AB)\): Là xác suất áo bị lỗi và thuộc phân xưởng I
\(P(AB) = P(A|B) \cdot P(B) \Leftrightarrow P(AB) = 0,02 \cdot 0,4 = 0,008\)
- Xác suất \(P(\bar AB)\): Là xác suất áo không bị lỗi và thuộc phân xưởng I
\(P(\bar AB) = P(\bar A|B) \cdot P(B) \Leftrightarrow P(\bar AB) = 0,98 \cdot 0,4 = 0,392\)
- Xác suất \(P(A\bar B)\): Là xác suất áo bị lỗi và thuộc phân xưởng II
\(P(A\bar B) = P(A|\bar B) \cdot P(\bar B) \Leftrightarrow P(A\bar B) = 0,03 \cdot 0,6 = 0,018\)
- Xác suất \(P(\bar A\bar B)\): Là xác suất áo không bị lỗi và thuộc phân xưởng II
\(P(\bar A\bar B) = P(\bar A|\bar B) \cdot P(\bar B) \Leftrightarrow P(\bar A\bar B) = 0,97 \cdot 0,6 = 0,582\)
b)
Xác suất lấy được áo bị lỗi trong lô hàng là:
\(P(A) = P(AB) + P(A\bar B) = 0,008 + 0,018 = 0,026\)
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cùng khám phá
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II".
a) Hoàn thành sơ đồ hình cây sau:
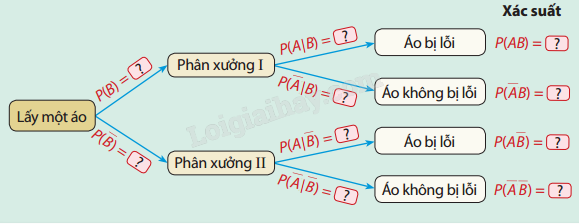
b) Ta nhận thấy biến cố A: "Lấy được áo bị lỗi" có thể xảy ra đồng thời với biến cố B: "Áo được sản xuất bởi phân xưởng I" hoặc biến cố B: "Áo được sản xuất bởi phân xưởng II". Người ta chứng minh được rằng: \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\). Hãy tính xác suất lấy được áo bị lỗi trong lô hàng.
Phương pháp giải:
a) Sử dụng công thức \(P(B|A) = \frac{{P(AB)}}{{P(A)}}\) hoặc \(P(AB) = P(B|A).P(A)\).
b) Sử dụng kết quả ở câu a và áp dụng công thức \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\) để tính xác suất.
Lời giải chi tiết:
a)
- Xác suất phân xưởng I sản xuất áo: \(P(B) = 0,4\)
- Xác suất phân xưởng II sản xuất áo: \(P(\bar B) = 0,6\)
- Xác suất áo bị lỗi từ phân xưởng I: \(P(A|B) = 0,02\)
- Xác suất áo bị lỗi từ phân xưởng II: \(P(A|\bar B) = 0.03\)
- Xác suất áo không bị lỗi từ phân xưởng I và phân xưởng II
Áo không bị lỗi từ phân xưởng I: \(P(\bar A|B) = 1 - P(A|B) \Leftrightarrow P(\bar A|B) = 1 - 0,02 = 0,98\)
Áo không bị lỗi từ phân xưởng II: \(P(\bar A|\bar B) = 1 - P(A|\bar B) \Leftrightarrow P(\bar A|\bar B) = 1 - 0.03 = 0,97\)
- Xác suất \(P(AB)\): Là xác suất áo bị lỗi và thuộc phân xưởng I
\(P(AB) = P(A|B) \cdot P(B) \Leftrightarrow P(AB) = 0,02 \cdot 0,4 = 0,008\)
- Xác suất \(P(\bar AB)\): Là xác suất áo không bị lỗi và thuộc phân xưởng I
\(P(\bar AB) = P(\bar A|B) \cdot P(B) \Leftrightarrow P(\bar AB) = 0,98 \cdot 0,4 = 0,392\)
- Xác suất \(P(A\bar B)\): Là xác suất áo bị lỗi và thuộc phân xưởng II
\(P(A\bar B) = P(A|\bar B) \cdot P(\bar B) \Leftrightarrow P(A\bar B) = 0,03 \cdot 0,6 = 0,018\)
- Xác suất \(P(\bar A\bar B)\): Là xác suất áo không bị lỗi và thuộc phân xưởng II
\(P(\bar A\bar B) = P(\bar A|\bar B) \cdot P(\bar B) \Leftrightarrow P(\bar A\bar B) = 0,97 \cdot 0,6 = 0,582\)
b)
Xác suất lấy được áo bị lỗi trong lô hàng là:
\(P(A) = P(AB) + P(A\bar B) = 0,008 + 0,018 = 0,026\)
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.
Phương pháp giải:
Sử dụng công thức tính xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\).
Lời giải chi tiết:
* Các biến cố:
\(A\): Biến cố lấy quả trắng lần đầu
\(\bar A\): Biến cố lấy quả đen lần đầu
\(B\): Biến cố lấy quả trắng lần thứ hai
Xác suất ban đầu:
\(P(A) = \frac{5}{{15}} = \frac{1}{3}\)
\(P(\bar A) = \frac{{10}}{{15}} = \frac{2}{3}\)
* Xác suất có điều kiện:
\(P(B|A) = \frac{4}{{14}} = \frac{2}{7}\)
\(P(B|\bar A) = \frac{5}{{14}}\)
* Công thức xác suất toàn phần: \(P(B) = P(A) \cdot P(B|A) + P(\bar A) \cdot P(B|\bar A)\)
Thay số: \(P(B) = \left( {\frac{1}{3} \cdot \frac{2}{7}} \right) + \left( {\frac{2}{3} \cdot \frac{5}{{14}}} \right) = \frac{2}{{21}} + \frac{{10}}{{42}} = \frac{2}{{21}} + \frac{5}{{21}} = \frac{7}{{21}} = \frac{1}{3}\)
Vậy xác suất lấy được quả cầu trắng lần thứ hai là: \(P(B) = \frac{1}{3}\)
Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 12 Cùng khám phá
Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.
Phương pháp giải:
- Sử dụng công thức xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\)
- Xác định tỉ lệ dân số nam và nữ
- Biết tỉ lệ mắc bệnh của từng giới
- Giải phương trình để tìm tỉ lệ nam mắc bệnh
Lời giải chi tiết:
* Xác định các biến cố:
\(A\): Biến cố là nam giới
\(B\): Biến cố là nữ giới
\(C\): Biến cố mắc bệnh bạch tạng
* Theo đề bài ta có các xác suất
\(P(A) = \frac{2}{5}\) ,\(P(B) = \frac{3}{5}\) ,\(P(C) = 0,45\% \),\(P(C|B) = 0,35\% \)
* Áp dụng công thức toàn phần
\(P(C) = P(A) \cdot P(C|A) + P(B) \cdot P(C|B)\)
\(0,45\% = (\frac{2}{5} \cdot P(C|A)) + (\frac{3}{5} \cdot 0,35\% )\)
* Giải Phương Trình
\(0,45\% = \frac{2}{5} \cdot P(C|A) + 0,21\% \)
\(0,45\% - 0,21\% = \frac{2}{5} \cdot P(C|A)\)
\(0,24\% = \frac{2}{5} \cdot P(C|A)\)
* Tính Tỉ Lệ Nam Mắc Bệnh
\(P(C|A) = \frac{{0,24\% \cdot 5}}{2}\)
\(P(C|A) = 0,6\% \)
Vậy tỉ lệ nam giới mắc bệnh bạch tạng là \(0,6\% \)
Mục 1 của SGK Toán 12 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là nền tảng để các em tiếp thu các kiến thức phức tạp hơn ở các chương tiếp theo. Chúng ta sẽ cùng nhau đi sâu vào từng bài tập, phân tích yêu cầu đề bài và tìm ra phương pháp giải tối ưu.
Bài tập này thường yêu cầu các em vận dụng kiến thức về... (giả sử bài tập liên quan đến đạo hàm). Để giải bài tập này, các em cần:
Lời giải chi tiết: (Cung cấp lời giải chi tiết cho bài tập 1, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng)
Bài tập này tập trung vào việc... (giả sử bài tập liên quan đến tích phân). Các em cần lưu ý:
Lời giải chi tiết: (Cung cấp lời giải chi tiết cho bài tập 2, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng)
Bài tập này yêu cầu các em ứng dụng kiến thức về... (giả sử bài tập liên quan đến hình học không gian). Để giải quyết bài toán này, các em có thể sử dụng:
Lời giải chi tiết: (Cung cấp lời giải chi tiết cho bài tập 3, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng)
Để đạt hiệu quả cao trong quá trình học và giải bài tập Toán 12 tập 2, các em cần:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp:
Hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 97, 98, 99 SGK Toán 12 tập 2. Chúc các em học tập tốt và đạt được kết quả cao nhất!