Chào mừng các em học sinh đến với bài giải bài tập 3.8 trang 103 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Trong 30 ngày, một nhà đầu tư đã theo dõi giá cổ phiếu của hai công ty G và H vào phiên mở cửa mỗi ngày. Thông tin được ghi lại ở hai bảng dưới đây:
Đề bài
Trong 30 ngày, một nhà đầu tư đã theo dõi giá cổ phiếu của hai công ty G và H vào phiên mở cửa mỗi ngày. Thông tin được ghi lại ở hai bảng dưới đây:
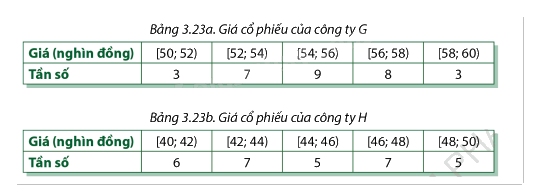
Giá cổ phiếu của công ty nào ít biến động hơn (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
Áp dụng các công thức sau để tính độ lệch chuẩn giá cổ phiếu của công ty G và H. Sau đó lấy hai giá trị này đem so sánh, công ty nào có độ lệch chuẩn thấp hơn thì giá cổ phiếu của công ty đó ít biến động hơn.
- Công thức tính trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)
Lời giải chi tiết
Theo đề bài, ta có N = 30.
Công ty G:

- Giá cổ phiếu trung bình là:
\({\bar x_G} = \frac{{51.3 + 53.7 + 55.9 + 57.8 + 59.3}}{{30}} \approx 55,07\)
- Tính \(\overline {x_G^2} \):
\(\overline {x_G^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{51}^2}.3 + {{53}^2}.7 + {{55}^2}.9 + {{57}^2}.8 + {{59}^2}.3}}{{30}} \approx 3037,53\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_G} = \sqrt {\overline {x_G^2} - {{\left( {{{\overline x }_G}} \right)}^2}} = \sqrt {3037,53 - 55,{{07}^2}} \approx 2,197\)
Công ty H:

- Giá cổ phiếu trung bình là:
\({\bar x_H} = \frac{{41.6 + 43.7 + 45.5 + 47.7 + 49.5}}{{30}} \approx 44,87\)
- Tính \(\overline {x_H^2} \):
\(\overline {x_H^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{41}^2}.6 + {{43}^2}.7 + {{45}^2}.5 + {{47}^2}.7 + {{49}^2}.5}}{{30}} \approx 2020,73\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_H} = \sqrt {\overline {x_H^2} - {{\left( {{{\overline x }_H}} \right)}^2}} = \sqrt {2020,73 - 44,{{87}^2}} \approx 2,777\)
Vì \({S_G} < {S_H}\) nên giá cổ phiếu của công ty G ít biến động hơn.
Bài tập 3.8 trang 103 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị, khoảng đơn điệu và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm.
Bài tập 3.8 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm:
Giải:
Việc giải bài tập 3.8 trang 103 SGK Toán 12 tập 1 giúp học sinh:
Bài tập 3.8 trang 103 SGK Toán 12 tập 1 là một bài toán quan trọng và cần thiết trong chương trình học Toán 12 tập 1. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh có thể tự tin giải bài tập này và đạt kết quả tốt nhất.