Chào mừng các em học sinh đến với bài giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
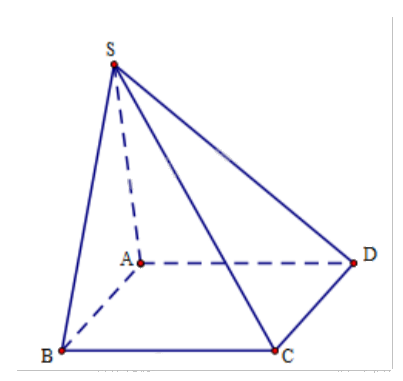
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình bình hành và phép biến đổi vectơ.
Lời giải chi tiết
Ta có thể viết:
\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} + \overrightarrow {BA} ) + (\overrightarrow {SD} + \overrightarrow {DC} )\)
Thay \(\overrightarrow {BA} = - \overrightarrow {AB} \) và \(\overrightarrow {DC} = - \overrightarrow {CD} \) vào biểu thức trên, ta được:
\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} - \overrightarrow {AB} ) + (\overrightarrow {SD} - \overrightarrow {CD} )\)
Sử dụng tính chất của hình bình hành:
\(\overrightarrow {AB} = \overrightarrow {DC} \quad {\rm{và}}\quad \overrightarrow {AD} = \overrightarrow {BC} \)
Nên ta có:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} - \overrightarrow {AB} + \overrightarrow {SD} + \overrightarrow {DC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Vậy đẳng thức \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) đã được chứng minh.
Bài tập 2.3 trang 64 SGK Toán 12 tập 1 là một phần quan trọng trong chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và các quy tắc tính đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức đạo hàm là nền tảng để giải quyết thành công bài tập này.
Bài tập 2.3 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 2.3 trang 64 SGK Toán 12 tập 1, chúng tôi xin trình bày lời giải chi tiết cho từng bài tập:
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Đề bài: Tìm đạo hàm cấp hai của hàm số g(x) = sin(x).
Lời giải:
g'(x) = cos(x)
g''(x) = -sin(x)
Đề bài: Tìm cực trị của hàm số h(x) = x2 - 4x + 3.
Lời giải:
h'(x) = 2x - 4
Giải phương trình h'(x) = 0, ta được x = 2.
h''(x) = 2 > 0, vậy hàm số đạt cực tiểu tại x = 2.
Giá trị cực tiểu là h(2) = -1.
Để giải bài tập đạo hàm một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Ngoài SGK Toán 12 tập 1, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Bài tập 2.3 trang 64 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ giải quyết thành công bài tập này và đạt kết quả tốt trong môn Toán.