Chào mừng các em học sinh đến với bài giải bài tập 3.5 trang 95 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.
Điều tra một số hộ gia đình thu nhập ở mức trung bình sinh sống trên hai địa bàn A, B, người ta thấy diện tích nhà ở của họ đều nhỏ hơn 100 m². Hai biểu đồ dưới biểu diễn kết quả thống kê. Số liệu về diện tích nhà ở của cư dân thuộc địa bàn nào phân tán hơn?
Đề bài
Điều tra một số hộ gia đình thu nhập ở mức trung bình sinh sống trên hai địa bàn A, B, người ta thấy diện tích nhà ở của họ đều nhỏ hơn 100 m². Hai biểu đồ dưới biểu diễn kết quả thống kê. Số liệu về diện tích nhà ở của cư dân thuộc địa bàn nào phân tán hơn?
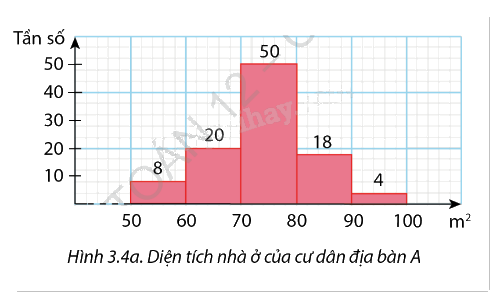
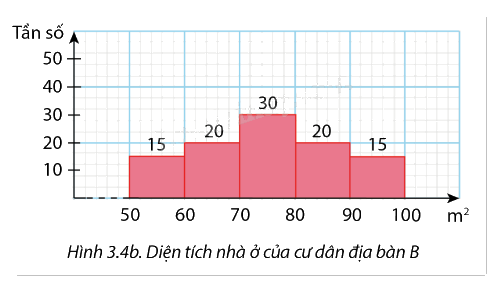
Phương pháp giải - Xem chi tiết
- Quan sát hai biểu đồ tần số.
- So sánh khoảng tứ phân vị và sự phân bố của các giá trị tần số.
- Địa bàn nào có khoảng tứ phân vị rộng hơn và độ phân bố các giá trị không đồng đều hơn thì dữ liệu tại đó sẽ phân tán hơn.
Lời giải chi tiết
Tổng số hộ gia đình trên hai địa bàn là 100.
Địa bàn A
- Tứ phân vị:
\(\frac{N}{4} = 25\) rơi vào nhóm [60; 70)
\({Q_1} = 60 + \frac{{25 - 8}}{{20}}.10 = 68,5\)
\(\frac{{3N}}{4} = 75\) rơi vào nhóm [70; 80)
\({Q_3} = 70 + \frac{{75 - 28}}{{50}}.10 \approx 79,4\)
- Khoảng tứ phân vị:
\(\Delta _Q^A = {Q_3} - {Q_1} = 79,4 - 68,5 \approx 10,9{m^2}\)
Địa bàn B
- Tứ phân vị:
\(\frac{N}{4} = 25\) rơi vào nhóm [60; 70)
\({Q_1} = 60 + \frac{{25 - 15}}{{20}}.10 = 65\)
\(\frac{{3N}}{4} = 75\) rơi vào nhóm [80; 90)
\({Q_3} = 80 + \frac{{75 - 65}}{{20}}.10 \approx 85\)
- Khoảng tứ phân vị:
\(\Delta _Q^B = {Q_3} - {Q_1} = 85 - 65 \approx 20{m^2}\)
Vì \(\Delta _Q^B > \Delta _Q^A\) nên diện tích nhà ở của cư dân thuộc địa bàn B phân tán hơn.
Bài tập 3.5 trang 95 SGK Toán 12 tập 1 thuộc chương trình học về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đạo hàm của hàm số, xét dấu đạo hàm và ứng dụng đạo hàm để khảo sát hàm số.
Bài tập 3.5 thường bao gồm các dạng bài sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập 3.5, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập. Các em có thể tham khảo lời giải này để tự giải các bài tập tương tự.
Để tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1, ta sử dụng các quy tắc tính đạo hàm cơ bản:
Áp dụng các quy tắc này, ta có:
y' = 3x2 - 4x + 5
Để hàm số f(x) = |x| có đạo hàm tại x = 0, ta cần kiểm tra giới hạn của tỷ số gia tăng tại x = 0:
limh→0 (f(0+h) - f(0))/h = limh→0 (|h| - 0)/h = limh→0 |h|/h
Tuy nhiên, giới hạn này không tồn tại vì:
limh→0+ |h|/h = 1 và limh→0- |h|/h = -1
Do đó, hàm số f(x) = |x| không có đạo hàm tại x = 0.
Để giải tốt các bài tập về đạo hàm, các em cần nắm vững các kiến thức sau:
Ngoài ra, các em nên luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải toán.
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 3.5 trang 95 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin hơn khi giải các bài tập tương tự.